memory-course
14 | CPU Cache:访存速度是如何大幅提升的?
你好,我是海纳。
经过上一节课的学习,我们了解到不同的物理器件,它们的访问速度是不一样的:速度快的往往代价高、容量小;代价低且容量大的,速度通常比较慢。为了充分发挥各种器件的优点,计算机存储数据的物理器件不会只选择一种,而是以CPU为核心,由内而外地组建了一整套的存储体系结构。它将各种不同的器件组合成一个体系,让各种器件扬长避短,从而形成一种快速、大容量、低成本的内存系统。
而我们要想写出高性能的程序,就必须理解这个存储体系结构,并运用好它。因此,今天这节课我们就来看看常见的存储结构是如何搭建的,并借此把握好影响程序性能的主要因素,从而对程序性能进行优化。
存储体系结构的核心
作为程序员,我们肯定是希望有无限资源的快速存储器,来存放程序的数据。而现实是,快速存储器的制造成本很高,速度慢的存储器相对便宜。所以从成本角度来说,计算机的存储结构被设计成分层的,一般包括寄存器、缓存、内存、磁盘等。
其中,缓存又是整个存储体系结构的灵魂,它让内存访问的速度接近于寄存器的访问速度。所以,要想深入理解存储体系结构,我们就要围绕“缓存”这个核心来学习。
在过去的几十年,处理器速度的增长远远超过了内存速度的增长。尤其是在2001~2005年间,处理器的时钟频率在以55%的速度增长,而同期内存速度的增长仅为7%。为了缩小处理器和内存之间的速度差距,缓存被设计出来。
我们说,距离处理器越近,访问速度就越快,造价也就越高,同时容量也会更小。缓存是处理器和内存之间的一个桥梁,通常分为多层,包括L1层、L2层、L3层等等。缓存的速度介于处理器和内存之间,访问处理器内部寄存器的速度在1ns以内(一个时钟周期),访问内存的速度通常在50~100ns(上百个时钟周期)之间。那么对于缓存来讲,靠近处理器最近的L1层缓存的访问速度在1ns~2ns(3个时钟周期)左右,外层L2和L3层的访问速度在10ns~20ns(几十个时钟周期)之间。
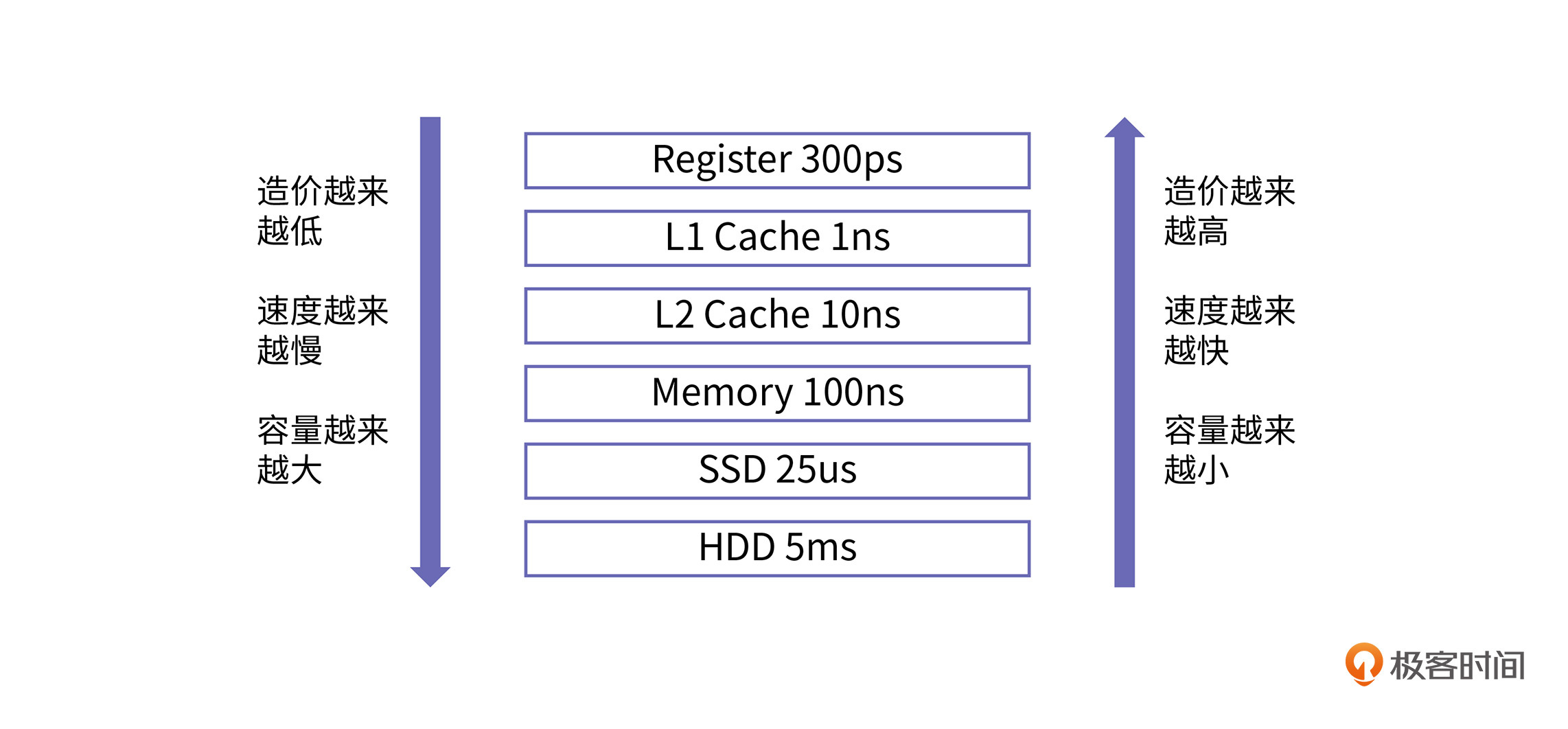
根据程序的空间局部性和时间局部性原理,一个处理得当的程序,缓存命中率要想达到70~90%并非难事。因此, 在存储系统中加入缓存,可以让整个存储系统的性能接近寄存器,并且每字节的成本都接近内存,甚至是磁盘。
可见缓存结合了寄存器速度快和内存造价低的优点,是整个存储体系的灵魂之所在。明白了这一点后,接下来我们拆解一下缓存的物理架构。
缓存的物理架构
缓存是由SRAM(静态随机存储)组成的,它的本质是一种时序逻辑电路,具体的每个单元(比特)由一个个锁存器构成,锁存器的功能就是让电路具有记忆功能,这一点我们在之前讲过。
SRAM的单位造价还是比较高的,而且要远高于内存的组成结构“DRAM(动态随机存储)”的造价。这是因为要实现一个锁存器需要六个晶体管,而实现一个DRAM仅需要一个晶体管和一个电容,但是DRAM因为结构简单,单位面积可以存放更多数据,所以更适合做内存。为了兼顾这两者的优缺点,于是它们中间需要加入缓存。
在制造方面,DRAM因为有电容的存在,不再是单纯的逻辑电路,所以不能用CMOS工艺制造,而SRAM可以。这也是为什么缓存可以集成到芯片内部,而内存是和芯片分开制造的。
在了解了缓存的内部构成之后,我们再来看看缓存是怎样集成到芯片上的。
缓存集成到芯片的方式有多种。在过去的单核时代,处理器和各级缓存都只有一个,因此缓存的集成方式相对单一,就是把处理器和缓存直接相连。2004年,Intel取消了4GHz奔腾处理器的研发计划,这意味着处理器以提升主频榨取性能的时代结束,多核处理器开始成为主流。
在多核芯片上,缓存集成的方式主要有以下三种:
- 集中式缓存:一个缓存和所有处理器直接相连,多个核共享这一个缓存;
- 分布式缓存:一个处理器仅和一个缓存相连,一个处理器对应一个缓存;
- 混合式缓存:在L3采用集中式缓存,在L1和L2采用分布式缓存。
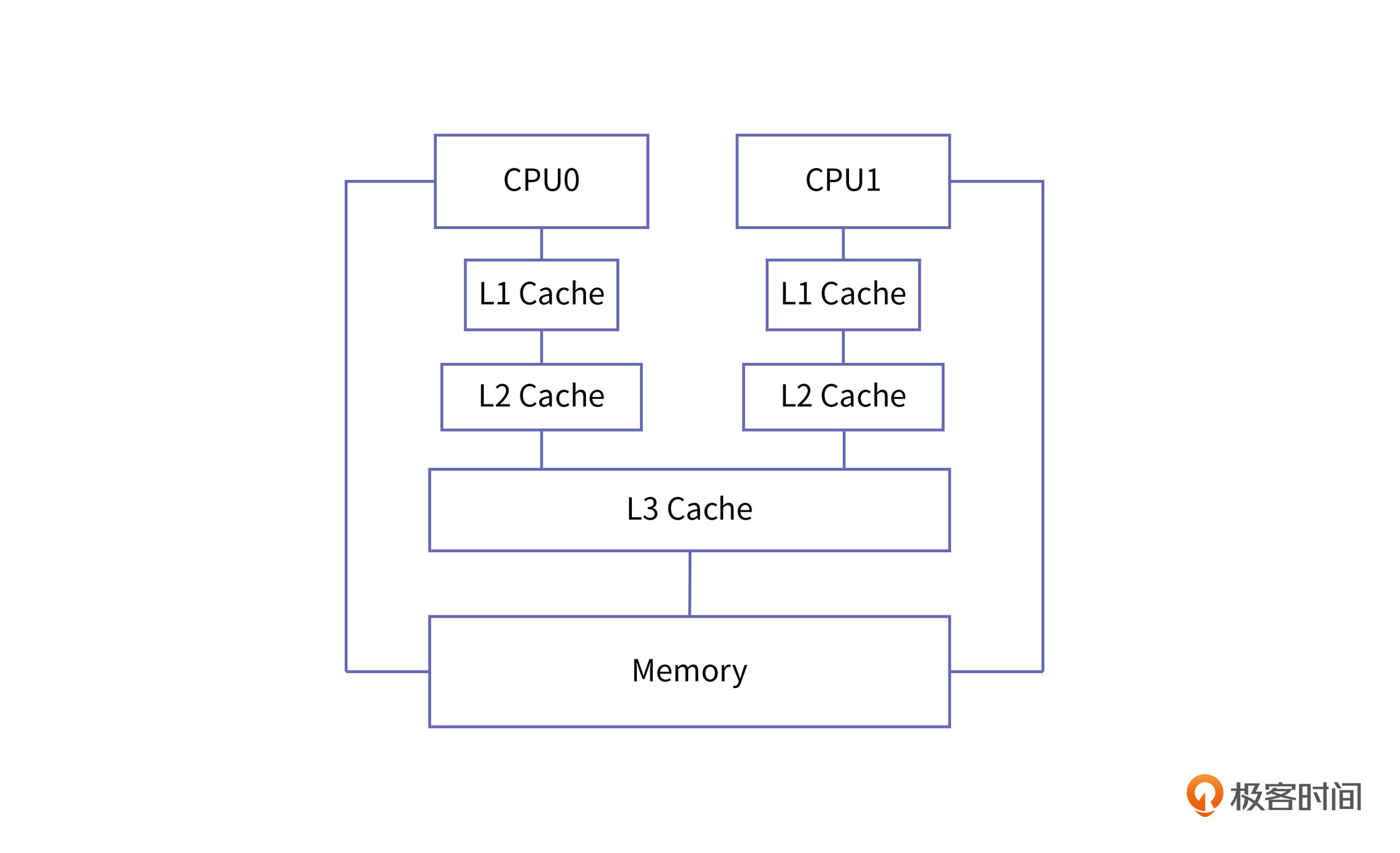
现代的多核处理器大都采用混合式的方式将缓存集成到芯片上,一般情况下,L3是所有处理器核共享的,L1和L2是每个处理器核特有的。
了解了缓存的物理架构后,我们来看一下缓存的工作原理
缓存的工作原理
首先,我们来理解一个概念,cache line。cache line是缓存进行管理的一个最小存储单元,也叫缓存块。从内存向缓存加载数据也是按缓存块进行加载的,一个缓存块和一个内存中相同容量的数据块(下称内存块)对应。这里,我们先从如何管理缓存块的角度,来看下缓存块的组织形式:
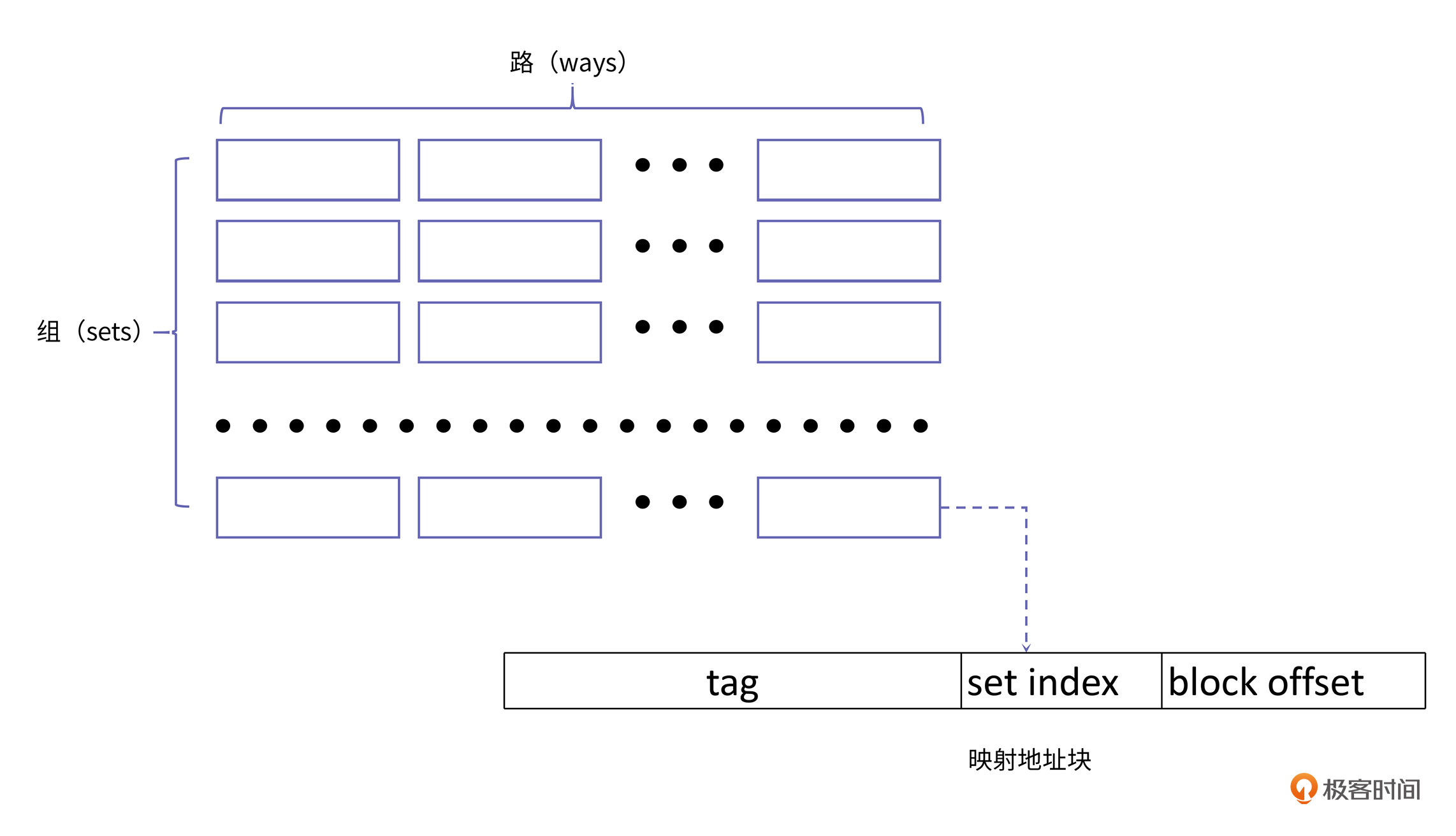
上图中的小方框就代表一个缓存块。从图中,你也可以看到,整个缓存由组(set)构成,每个组由路(way)构成。所以整个缓存容量等于组数、路数和缓存块大小的乘积:
$整个缓存容量=组数\times路数\times缓存块大小$
为了简化寻址方式,内存地址确定的数据块总是会被放在一个固定的组,但可以放在组内的任意路上,也就是说,对于一个特定地址数据的访问,它如果要载入缓存,那么它放在上图中的行数是固定的,但是具体放到哪一列是不固定的。根据缓存中组数和路数的不同,我们将缓存的映射方式分为三类:
- 直接相连映射:缓存只有一个路,一个内存块只能放置在特定的组上;
- 全相连映射:缓存只有一个组,所有的内存块都放在这一个组的不同路上;
- 组组相连映射:缓存同时由多个组和多个路。
对于直接相连映射,当多个内存块映射到同一组时,会产生冲突,因为只有一列,这个时候就需要将旧的缓存块换出,同时将新的缓存块放入,所以 直接相连映射会导致缓存块被频繁替换。
而 全相连映射可以在很大程度上避免冲突,不过,当要查询某个缓存块时,需要逐个遍历每个路,而且电路实现也比较困难。一个折中的办法就是,采用组组相连映射。这种方式与直接相连映射相比,产生冲突的可能性更小,与全相连映射相比,查询效率更高,实现也更简单。
上面的举例比较简单,我们再来看这样一种情况:缓存的组数一直是$2^{n}$。虽然组数为$2^{n}$利于查询和定位,但是如果一个程序刚好以$2^{n}$间隔寻址,就会导致地址更多的被映射到同一个组,而另外一些组就会被映射得很少。因此,也有些缓存的组数会设计成一个质数,这样即便程序以$2^{n}$间隔寻址,落到相同组的可能性会大大减小,这样一来,缓存各个组的利用率就会相对均衡。
那一个内存块具体是怎样映射到一个缓存块的呢?我们先来看看缓存块的内部结构:
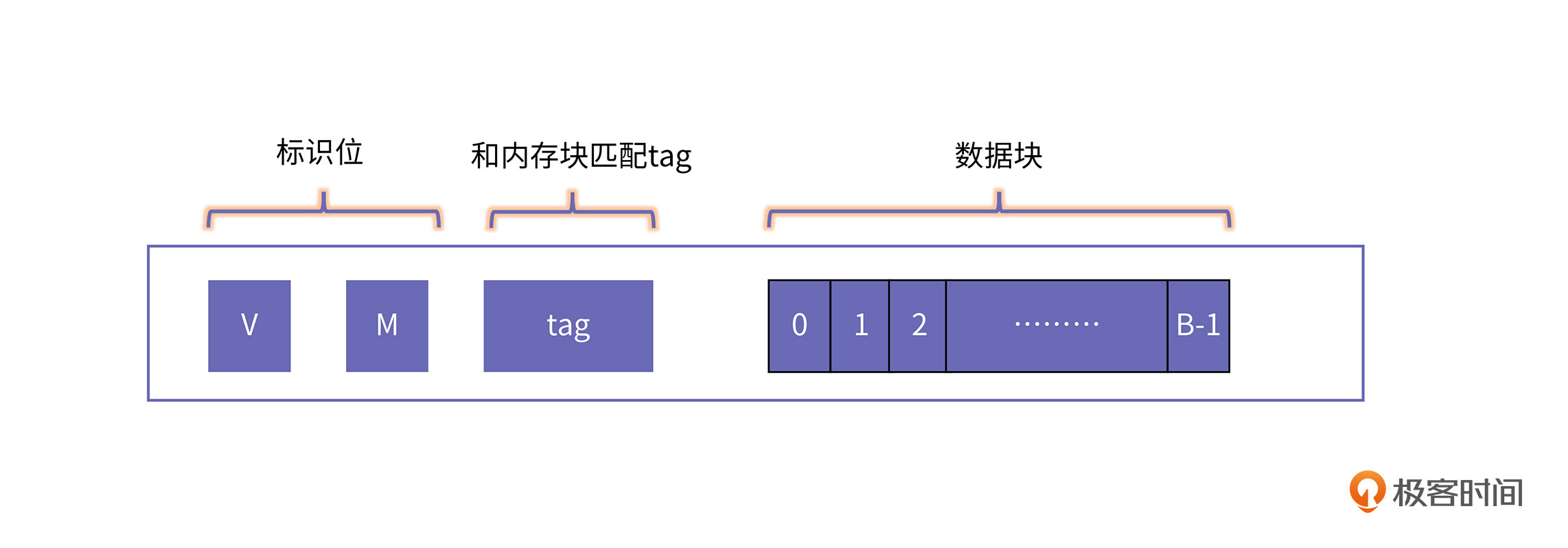
其中,V(valid)表示这个缓存块是否有效,或者说是否正在被使用;M(modified)表示这个缓存块是否被写,也就是“脏”位;B表示缓存块的bit个数。
假设要寻址一个32位的地址,缓存块的大小是64字节,缓存组织方式是4路组相连,缓存大小是8K。经过计算我们得到缓存一共有32个组($8\times1024\div64\div4=32$)。那么对于任意一个32位的地址Addr ,它映射到缓存的组号(set index)为 Addr对组数32取模,组号同时也等于Addr的第6~10位( (Addr » 6) & 0x1F ),Addr的低6位很好理解,它是缓存块的内部偏移($2^{6}$为64字节),那么高21位是用来干嘛的呢?我们接着往下看。
确定需要被映射到哪个组之后,我们需要在该组的路中进行查询。查询方式也很简单,直接将每个缓存块tag的bit位和地址Addr的高21位逐一进行匹配。如果相等,就说明该内存块已经载入到缓存中;如果没有匹配的tag,就说明缓存缺失,需要将内存块放到该组的一个空闲缓存块上;如果所有路的缓存块都正在被使用,那么需要选择一个缓存块,将其移出缓存,把新的内存块载入。
上面这个过程涉及到缓存块状态转换,而状态转换又涉及到有效位V、脏位M、标签tag。总体来讲,缓存的状态转换有以下几种情况:
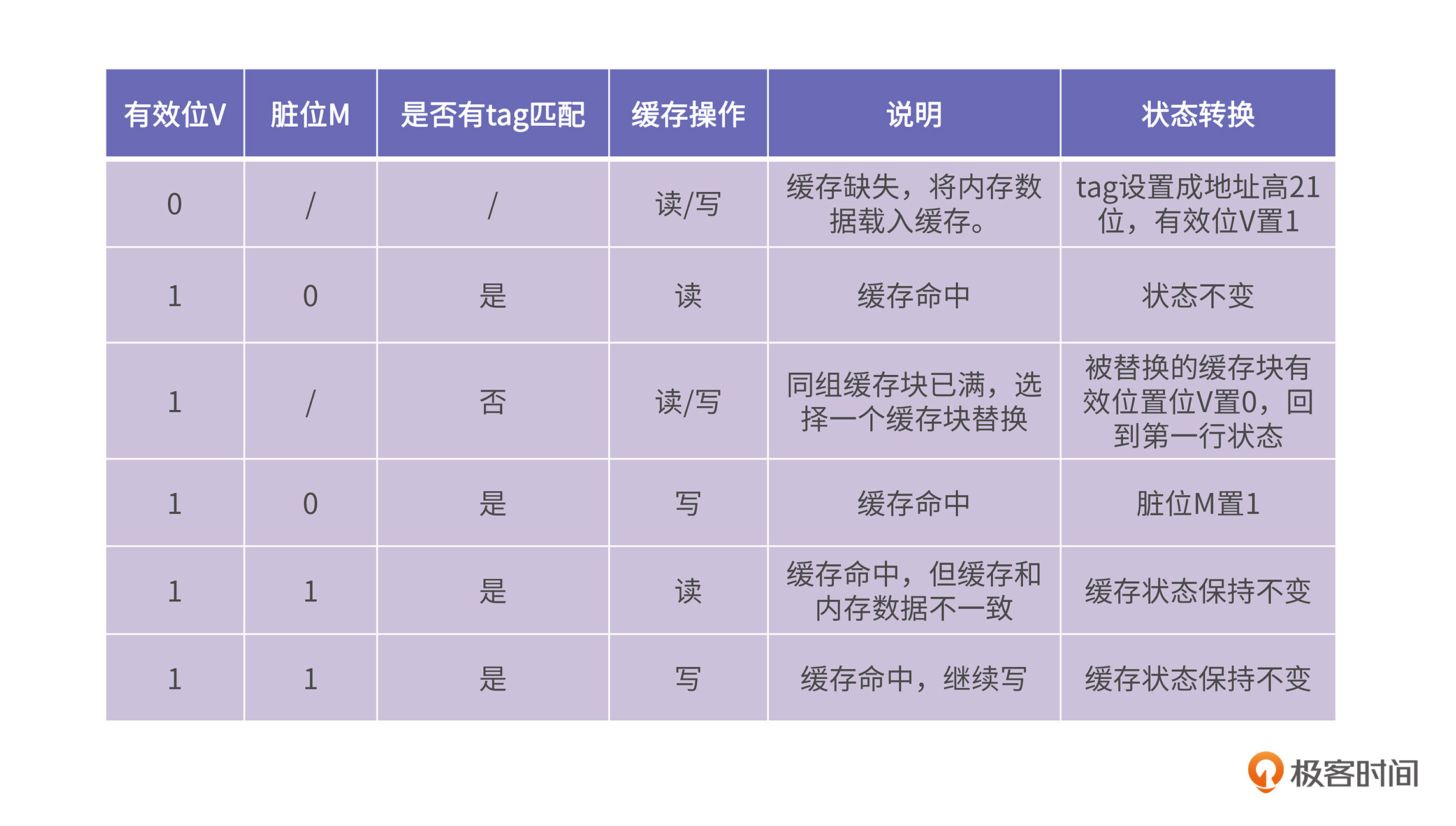
这里我们提到了缓存块替换,当同组的缓存块都被用完时,需要选择一个缓存块被换出,那么应该选谁被换出呢?这就和缓存块替换策略有关了。
缓存块替换策略
缓存块替换策略需要达到的一个目标是: 被替换出的数据块应该是将来最晚会被访问的块。然而,对将来即将发生的事情是没有办法预测的,因为处理器并不知道程序将来会访问哪个地址。因此, 现在的缓存替换策略都采用了最近最少使用算法(Least Recently Used ,LRU)或者是类似LRU的算法。
LRU的原理很简单,比如程序要顺序访问 B1 、B2、B3、B4、B5这几个地址块,并且这几个缓存块都映射到缓存的同一个组,同时我们假设缓存采用4路组组相连映射,那么当访问B5时,B1就需要被替换出来。要实现这一点,有很多种方式,其中最简单也最容易实现的是利用位矩阵来实现。
首先,我们定义一个行、列都与缓存路数相同的矩阵。当访问某个路对应的缓存块时,先将该路对应的所有行置为1,然后再将该路对应的所有列置为0。最终结果体现为,缓存块访问时间的先后顺序,由矩阵行中1的个数决定,最近最常访问缓存块对应行1的个数最多。
假设现在一个四路相连的缓存组包含数据块 B1、B2、B3、B4, 数据块的访问顺序为 B2、B3、B1、B4,那么LRU矩阵在每次访问后的变化如下图所示:
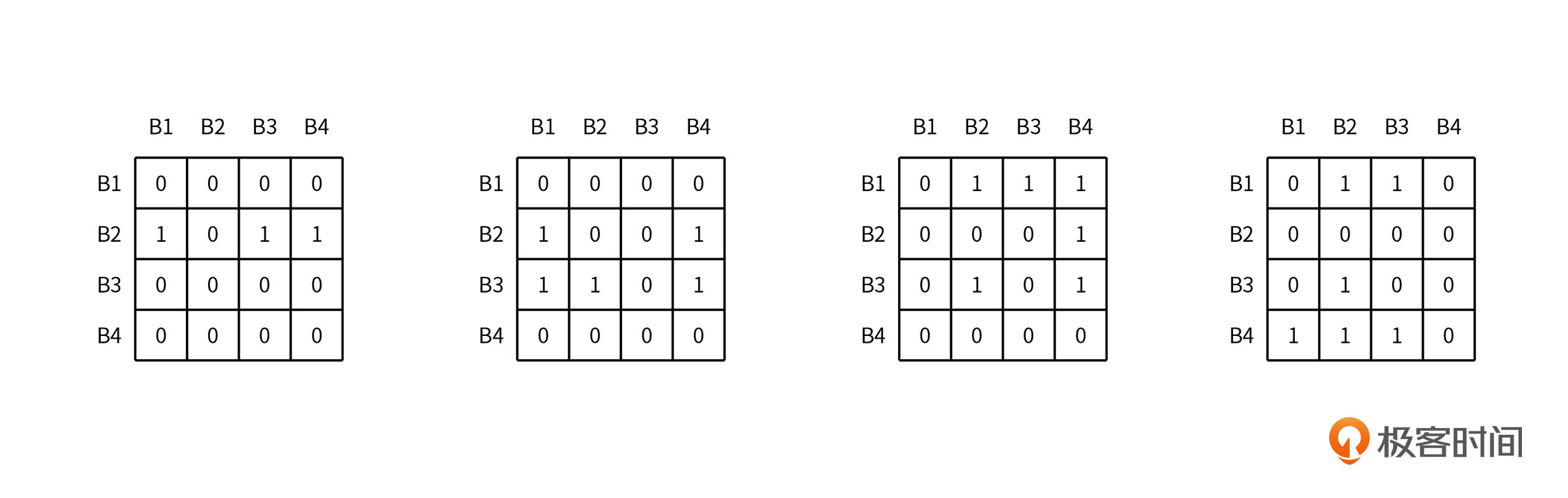
你会发现,最终B2对应行的1的个数最少,所以B2将会被优先替换。
在理解了缓存结构和它的工作原理以后,我们就可以来讨论这节课的核心内容了:如何正确地使用缓存,才可以写出高性能的程序?
缓存对程序性能的影响
通过前面的分析,我们已经知道,CPU将未来最有可能被用到的内存数据加载进缓存。 如果下次访问内存时,数据已经在缓存中了,这就是缓存命中,它获取目标数据的速度非常快。如果数据没在缓存中,这就是缓存缺失,此时要启动内存数据传输,而内存的访问速度相比缓存差很多。所以我们要避免这种情况。下面,我们先来了解一下哪些情况容易造成缓存缺失,以及具体会对程序性能带来怎样的影响。
缓存缺失
缓存性能主要取决于缓存命中率,也就说缓存缺失(cache miss)越少,缓存的性能就越好。一般来说,引起缓存缺失的类型主要有三种:
- 强制缺失:第一次将数据块读入到缓存所产生的缺失,也被称为冷缺失(cold miss),因为当发生缓存缺失时,缓存是空的(冷的);
- 冲突缺失:由于缓存的相连度有限导致的缺失;
- 容量缺失:由于缓存大小有限导致的缺失。
第一类强制缺失最容易理解,因为第一次将数据读入缓存时,缓存中不会有数据,这种缺失无法避免。
第二类冲突缺失是因为相连度有限导致的,这里我用一个例子给你说明一下。在这个例子中,第一步我们可以通过getconf命令查看缓存的信息:
# getconf -a |grep CACHE
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
LEVEL1_ICACHE_SIZE 32768
LEVEL1_ICACHE_ASSOC 8
LEVEL1_ICACHE_LINESIZE 64
LEVEL1_DCACHE_SIZE 32768
LEVEL1_DCACHE_ASSOC 8
LEVEL1_DCACHE_LINESIZE 64
LEVEL2_CACHE_SIZE 262144
LEVEL2_CACHE_ASSOC 4
LEVEL2_CACHE_LINESIZE 64
LEVEL3_CACHE_SIZE 3145728
LEVEL3_CACHE_ASSOC 12
LEVEL3_CACHE_LINESIZE 64
LEVEL4_CACHE_SIZE 0
LEVEL4_CACHE_ASSOC 0
LEVEL4_CACHE_LINESIZE 0
在这个缓存的信息中,L1Cache(LEVEL1_ICACHE和LEVEL1_DCACHE分别表示指令缓存和数据缓存,这里我们只关注数据缓存)的cache line 大小为64字节,路数为8路,大小为32K,可以计算出缓存的组数为64组($32K\div8\div64=64$)。
第二步,我们使用一个程序来测试缓存的影响:
// cache.c
#include <stdio.h>
#include <stdlib.h>
#define M 64
#define N 10000000
int main( )
{
printf("%ld",sizeof(long long));
long long (*a)[N] = (long long(*)[N])calloc(M * N, sizeof(long long));
for(int i = 0; i < 100000000; i++) {
for(int j = 0; j < 4096; j+=512) {
a[5][j]++;
}
}
return 0;
}
上面代码中定义了一个二维数组,数组中元素的类型为long long ,元素大小为8字节。所以一个cache line 可以存放 $64\div8$=$8$个元素。一组是8路,所以一组可以存放$8\times8$=$64$个元素。一路包含64个cache line,因为前面计算出缓存的组数为64,所以一路可以存放$8\times64$=$512$个元素。
代码中的第一层循环是执行次数,第二层循环是以512 为间隔访问元素,即每次访问都会落在同一个组内的不同cache line ,因为一组有8路,所以我们迭代到 $512\times8$=$4096$的位置。这样可以使同一组刚好可以容纳二层循环需要的地址空间。运行结果如下:
# gcc cache.c
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
# time ./a.out
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
8
real 0m2.670s
user 0m2.671s
sys 0m0.001s
第三步,当我们将第二层循环的迭代次数扩大一倍,也就是8192时,运行结果如下:
# gcc cache.c
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
# time ./a.out
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
8
real 0m16.693s
user 0m16.700s
sys 0m0.001s
虽然运算量增加了一倍,但运行时间却增加了6倍,相当于性能劣化三倍。劣化的根本原因就是当i > 4096时,也就是访问4096之后的元素,同一组的cache line 已经全部使用,必须进行替换,并且之后的每次访问都会发生冲突,导致缓存块频繁替换,性能劣化严重。
第三类缓存容量缺失,可以认为是除了强制缺失和冲突缺失之外的缺失,也很好理解,当程序运行的某段时间内,访问地址范围超过缓存大小很多,这样缓存的容量就会成为缓存性能的瓶颈,这里要注意和冲突缺失加以区别,冲突缺失指的是在同一组内的缺失,而容量缺失描述范围是整个缓存。
程序局部性
在 第1节课 里,我们已经讲过,程序局部性分为时间局部性和空间局部性。如果程序有非常好的局部性,那么在程序运行期间,缓存缺失就很少发生。
我们对上面的例子进行修改,以此来验证程序局部性对缓存命中率的影响,进一步可以观察它对性能产生怎样的影响。
#include <stdio.h>
#include <stdlib.h>
#define M 10000
#define N 10000
int main( )
{
printf("%ld",sizeof(long long));
long long (*a)[N] = (long long(*)[N])calloc(M * N, sizeof(long long));
for(int i = 0; i < M; i++) {
for(int j = 0; j < N; j++) {
a[i][j]++;
}
}
return 0;
}
这里主要进行了两处修改: 一是修改了迭代次数,方便测试;二是将之前间隔访问数组中的部分元素修改为顺序访问整个数组,访问方式按二维数组的行逐次访问。测试结果如下:
# gcc -O0 cache.c
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
# time ./a.out
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
8
real 0m1.245s
user 0m0.797s
sys 0m0.449s
但当我们按列访问时,也就是将内层循环条件提到外面:
for(int j = 0; j < N; j++) {
for(int i = 0; i < M; i++) {
a[i][j]++;
}
}
运行结果为:
# gcc -O0 cache.c
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
# time ./a.out
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
8
real 0m2.527s
user 0m1.980s
sys 0m0.548s
可以看到,性能也出现了2倍的劣化,这次劣化的主要原因是当按行访问时地址是连续的,下次访问的元素和当前大概率在同一个cache line(一个元素8字节,而一个cache line 可以容纳8个元素),但是当按列访问时,由于地址跨度大,下次访问的元素基本不可能还在同一个cache line,因此就会增加cache line被替换的次数,所以性能劣化。
你需要注意的是, 这次编译选项都添加了-O0选项,告诉编译器不要进行优化,因为现在的编译器很聪明,能够识别出这种循环外提的优化,所以我们要先关掉优化。
在理解了缓存缺失对程序性能的影响后,我们来看一类非常典型的因为缓存使用不当而引起的性能下降的问题,这类问题统称为伪共享。
伪共享
伪共享(false-sharing)的意思是说, 当两个线程同时各自修改两个相邻的变量,由于缓存是按缓存块来组织的,当一个线程对一个缓存块执行写操作时,必须使其他线程含有对应数据的缓存块无效。这样两个线程都会同时使对方的缓存块无效,导致性能下降。
我们具体来看这样一个例子:
#include <stdio.h>
#include <pthread.h>
struct S{
long long a;
long long b;
} s;
void *thread1(void *args)
{
for(int i = 0;i < 100000000; i++){
s.a++;
}
return NULL;
}
void *thread2(void *args)
{
for(int i = 0;i < 100000000; i++){
s.b++;
}
return NULL;
}
int main(int argc, char *argv[]) {
pthread_t t1, t2;
s.a = 0;
s.b = 0;
pthread_create(&t1, NULL, thread1, NULL);
pthread_create(&t2, NULL, thread2, NULL);
pthread_join(t1, NULL);
pthread_join(t2, NULL);
printf("a = %lld, b = %lld\n", s.a, s.b);
return 0;
}
在这个例子中,main函数中创建了两个线程,分别修改结构体S中的a 、b 变量。a 、b均为long long 类型,都占8字节,所以a 、b 在同一个cache line中,因此会发生为伪共享的情况。程序的运行结果为:
# gcc -Wall false_sharing.c -lpthread
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
# time ./a.out
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
a = 100000000, b = 100000000
real 0m0.790s
user 0m1.481s
sys 0m0.008s
解决伪共享的办法是,将a 、b不要放在同一个cache line,这样两个线程分别操作不同的cache line 不会相互影响。具体来讲,我们需要对结构体S做出如下修改:
struct S{
long long a;
long long nop_0;
long long nop_1;
long long nop_2;
long long nop_3;
long long nop_4;
long long nop_5;
long long nop_6;
long long nop_7;
long long b;
} s;
因为在a、b中间插入了8个long long类型的变量,中间隔了64字节,所以a、b会被映射到不同的缓存块,程序执行结果如下:
# gcc -Wall false_sharing.c -lpthread
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
# time ./a.out
<audio src='./14-CPUCache:访存速度是如何大幅提升的?.mp3' controls></audio>
a = 100000000, b = 100000000
real 0m0.347s
user 0m0.693s
sys 0m0.001s
在这个结果中,你可以看到,性能有一倍的提升。
其实,伪共享是一种典型的缓存缺失问题,在并发场景中很常见。 在Java的并发库里经常会看到为了解决伪共享而进行的数据填充。这是大家在写并发程序时也要加以注意的。
总结
今天这节课,我们先介绍了存储体系结构的架构和工作原理。其中,缓存又是整个存储体系结构的灵魂,它让内存访问的速度接近于寄存器的访问速度。缓存对程序员是透明的,程序员不必使用特定的API接口来操作缓存工作,它是自动工作的。但如果我们的代码写得不好的话,我们就会感受到缓存不能起作用时的性能下降了。
缓存的映射方式包括了直接相连、全相连、组组相连三种。直接相连映射会导致缓存块被频繁替换;而全相连映射可以很大程度上避免冲突,但查询效率低;组组相连映射,与直接相连映射相比,产生冲突的可能性更小,与全相连映射相比,查询效率更高,实现也更简单。
如果要访问的数据不在缓存中,这就是缓存缺失。当发生缓存缺失时,就需要往缓存中加载目标地址的数据。如果缓存空间不足了,就需要对缓存块进行替换,替换的策略多采用LRU策略。
缓存缺失对性能影响非常大。缓存缺失主要包括强制缺失,冲突缺失和容量缺失。为了避免缓存缺失我们一定要注意程序的局部性,虽然编译器会帮我们做很多事情,但编译器还是有很多情况是无法优化的。
伪共享是一类非常典型的缓存缺失问题。它是由于多个线程都反复使对方的缓存块无效,带来的性能下降。为了解决这一类问题,我们可以考虑让多个线程所共同访问的对象,在物理上隔离开,保证它们不会落在同一个缓存块里。
好了,这节课到这里就结束了。下节课,我将带你探讨缓存一致性问题是如何解决的。
思考题
cache被翻译成缓存,buffer被翻译成缓冲区。那么,请你思考一下,cache和buffer这两个词的区别是什么?它们分别用在什么场景下?除了我们这节课所讲的物理缓存外,你还知道哪些缓存结构?

好啦,这节课到这就结束啦。欢迎你把这节课分享给更多对计算机内存感兴趣的朋友。我是海纳,我们下节课再见!