dynamic-programming-course
08|子数组问题:从解决动归问题套路到实践解题思路
你好,我是卢誉声。
如果你已经通过前面的课程,掌握了背包问题的奥义,那么恭喜你已经正式跨过动态规划的门槛了。除了背包问题以外,我们还需要掌握剩下几个类型的动态规划问题。
其中有一个是子数组问题,另一个是子序列问题。今天,我们就从子数组问题开始讲起,这类问题很容易在技术面试中出现,让我们来看一看如何用动归问题的套路来应对面试中的常见问题。
在前面的课程中,我们根据直觉设计了备忘录的定义。但事实上,这个备忘录的定义也是有讲究的。因此,在开始今天的课程前,有这样一个问题值得你关注: 备忘录的定义会对编写代码产生什么影响呢?
让我们带着这个疑问,来学习今天的内容吧。
什么是子数组问题?
首先,我们要明确一下什么是动态规划中的子数组问题。如果一道题目给定的输入是一个数组,那么满足以下条件的问题就是动归子数组问题:
- 问题符合动归典型特征:
a. 求“最”优解问题(最大值和最小值);
b. 求可行性(True 或 False);
c. 求方案总数。
- 题目的答案是题设数组的子数组,或者来源于子数组。
所谓答案来源于子数组,举个简单例子。比如这节课要讲到的最大子数组之和的问题,我们要求的答案就是子数组每个数字相加得到的。这个答案来源于子数组,只是对子数组多做了一步加法而已。
我在这里给出的定义同样是经验总结,所以它在 90% 以上的情况下是工作的,它足以应对面试中遇到的问题。
了解了什么是子数组问题后,现在让我们来看一看典型的面试问题。
回文子串个数
我们先来看一看回文子串问题的描述。
问题:给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例1:
输入:"dp"
输出:2
解释:共有两个回文子串,分别为 "d", "p"。
示例2:
输入:"aaa"
输出:6
解释:共有六个回文子串,分别为 "a", "a", "a", "aa", "aa", "aaa"。注意题设,具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串,因此像 "aa" 和 "aa" 就是两个不同的回文子串。
算法问题分析
字符串当然可以理解成数组。从数据结构上讲,它也是连续的,也可以通过索引访问特定位置字符。
除此之外,我们还需要注意一个子数组问题的特征,即答案也必须是连续的。举个例子,如果输入的字符串是”abca”,那么”aca”是原问题的答案吗?不是,因为”aca”是一个子序列,它不连续。有关于子序列的问题会比子数组稍微复杂一些,我会在下一课进行讲解。

那么,这是一个动态规划问题吗?显然,最笨拙的一种方法是穷举,然后再编写一个 Helper 函数来判断穷举出的子字符串是否是回文。但这样效率太低了,我们需要考虑更高效的方法。
为了高效地进行穷举操作,我们需要考虑使用动态规划来解。仿照之前的做法,我们对该问题做一个分析,看看它是否满足求解动态规划的特征。
- 重叠子问题:在穷举的过程中肯定存在重复计算的问题。这是因为各种排列组合间肯定存在重叠子问题的情况;
- 无后效性:对不是最长的回文子数组,一定包含在更长的回文子数组中,而更长的回文子数组不会包含在较短的回文子数组中,依赖是单项的;
- 最优子结构:对整个字符串,其最长的回文子串肯定包含了更短长度字符串中的回文子串,子问题可以递归求解。
既然是动归问题,接下来我们看看该如何写出状态转移方程吧。
写出状态转移方程
我们根据之前总结的动态规划求解模板,来看看如何解决这个问题。
首先,我们先来确定 初始化状态。从问题的示例就可以看出(当然也很容易想到),单个字符一定是它自己的回文。
接着,再来确定 状态参数。由于我们需要在整个字符串(数组)中确定子串(子数组)的位置,因此需要两个变量来约束和确定子串,一个是子串的起始位置,另一个是结束位置。在算法的执行过程中,起始和结束位置是变化的,因此它们是状态参数。
既然有两个状态参数,因此我们考虑使用二维数组作为动归解法的备忘录。设 $DP[i][j]$,其中 $i$ 是子数组的起始位置,$j$ 是结束位置,而 $DP[i][j]$ 又代表什么含义呢?
这里我们需要分析一下。我们说,动态规划的当前问题是根据它的子问题 ➕ 当前决策推导出来的。从数组的角度上看,无非就是:一个范围较小的回文子数组 ➕ 额外元素后,再看它是不是回文子数组。这么说有些抽象,我画了一张图,你看一看就明白了。
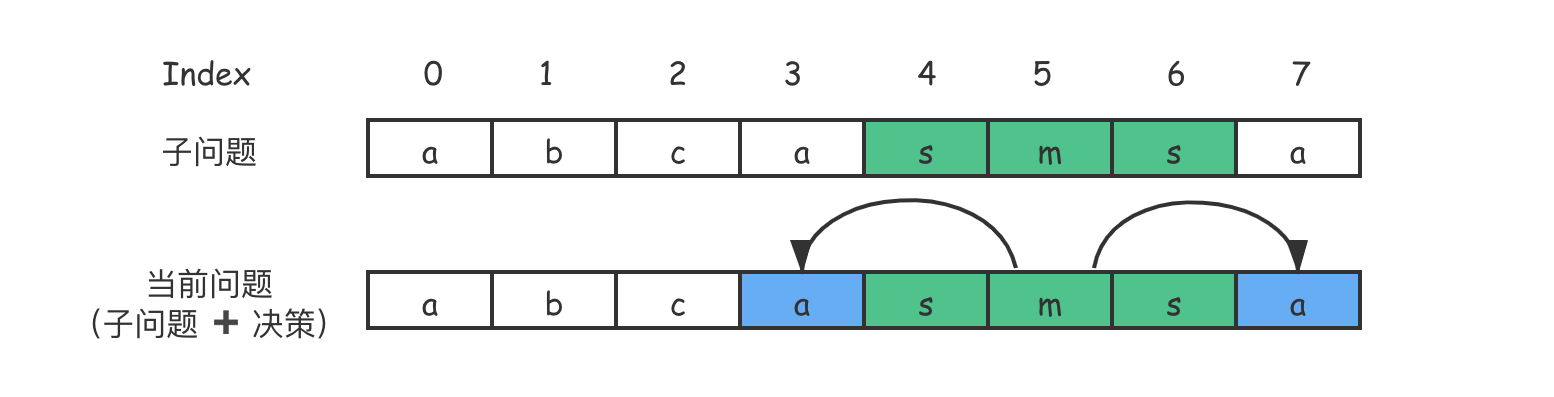
从图中可以看到,更大范围的问题是由前面的子问题 ➕ 当前决策推导出来的,当前的 决策 就是如果向子问题的两边分别扩充一个元素,那么当前问题是否还是回文呢?
在上图给出的示例中,当前问题仍然是回文,如果设 $DP[4][6]$ 为子问题,那么当前问题 $DP[3][7]$ = $DP[4][6]$ + 决策。现在问题已经很明显了,这个决策就是 True 或者 False。
因此, $DP[i][j]$ 所对应的值是子串 $i…j$ 是否为回文(True 或 False)。
一切就绪了,现在给出回文子串问题的状态转移方程。你会发现,相较我前面的背包问题来说,这里的方程比较简单。我们把字符串当作数组来访问,当 $s[i] == s[j]$ 时,当前子问题的答案就是 $DP[i+1][j-1]$ && $s[i] == s[j]$(其中 $s[i] == s[j]$ 即为 True,因此在状态转移方程中没有写出来);而当 $s[i] != s[j]$ 时,显然当前子问题的答案就是 False。
\[DP(i, j)=\\left\\{\\begin{array}{c} DP\[i+1\]\[j-1\],s\[i\]==s\[j\]\\\\ False, s\[i\] \\ne s\[j\] \\end{array}\\right.\]编写代码进行求解
所有先决条件都解决了,现在我们来看一下如何用标准的动归解法来求解此问题,我直接给出代码。
Java 实现:
int countSubstrings(String s) {
int n = s.length();
if (0 == n) return 0;
int ans = 0;
boolean[][] dp = new boolean[n][n];
for (int i = 0; i < n; i++) {
dp[i][i] = true;
ans++;
}
for (int j = 1; j < n; j++) {
for (int i = 0; i < j; i++) {
dp[i][j] = (s.charAt(i) == s.charAt(j)) && (j-i <3 || dp[i+1][j-1]);
if (dp[i][j]) { ans++; }
}
}
return ans;
}
C++ 实现:
int CountSubstrings(string s) {
int n = static_cast<int>(s.size());
if (0 == n) return 0;
int ans = 0;
bool dp[n][n]; memset(dp, 0, sizeof(dp));
for (int i = 0; i < n; i++) {
dp[i][i] = true;
ans++;
}
for (int j = 1; j < n; j++) {
for (int i = 0; i < j; i++) {
dp[i][j] = s[i]==s[j] && (j-i <3 || dp[i+1][j-1]);
if (dp[i][j]) { ans++; }
}
}
return ans;
}
我们在第 2 行到第 10 行创建了备忘录,并进行了初始化状态的操作,即每一个单个字符都是回文,即每个 $dp[i][i]$ 对应的值都是 True。同时,原问题问的是有多少个回文子串,因此我们创建了 ans 变量用来存储答案,并在初始化状态时就对其进行了自增(这是因为这些单字符的子问题都是答案,它们对应的值为 True)。
接下来,我们从起始位置 0 到结束位置 1,起始位置 0 到结束位置 2 … 起始位置 n-1 到结束位置 n 进行遍历,并按照状态转移方程的“指示”来进行子问题的计算。
这看起来没有什么问题,无非就是穷举所有可能,并自底向上地用备忘录加速我们的计算。但如果你仔细阅读了代码的第 14 行,你就会发现,我们的处理方法跟上面的状态转移方程有些区别。
事实上,在编写这个问题的状态转移方程时,有技巧可以利用。我们仍然分析以下回文的特征:
- 当子问题局限于单字符时,它一定是回文(如 “a”),因此子问题的答案是 True;
- 当子问题是由相同的两个字符构成的,它一定是回文(如 “aa”),因此子问题的答案是 True;
- 当子问题是由左右两个相同字符外加一个任意字符,共三个字符构成时,它一定是回文(如 “aba”),因此子问题的答案是 True。
综上所述,只要 $s[i] == s[j]$ 且 $j - i$ < $3$ 的时候,那个子问题一定是回文,其对应的 $dp[i][j]$ 一定是 True。因此,我们对状态转移方程做一个调整:
\[DP(i, j)=\\left\\{\\begin{array}{c} DP\[i+1\]\[j-1\],s\[i\]==s\[j\]\\\\ s\[i\]==s\[j\] \\&\\& j-i<3, s\[i\] \\stackrel{?}{=} s\[j\] \\end{array}\\right.\]这样一来,我们就用比较优雅的方式解决了回文子串问题。算法的时间复杂度为 O(n2),空间复杂度为 O(n2)。
从题目的标题我们可以看出,最长回文子串问题属于动态规划当中的求方案个数的问题。但没有题目的时候你能判断出来它的类型吗?
这里有些迷惑性,因为我们在处理子问题的时候,其对应存储在备忘录中的值是 True 或 False。我们只是在备忘录中用 True 或 False 存储了中间计算的状态,这个缓存的值只是中间计算结果,这跟我们前面遇到的问题中存储数字是一个思路(你甚至可以不用 True 或 False,而使用 0 和 1 来表示中间计算的结果)。
同时,我们可以发现,DP 数组的定义在这个问题下比较特别,虽然是一个数组的问题,但是我们需要两个变量来定义(约束)子串,而子串的位置是跟随算法的执行来回漂移的。
所以,记住这个关键点:如果问题涉及位置,考虑增加备忘录的维度来记录下会发生变化的这些变量。这些变量就是状态转移方程中最为关键的状态参数,一般每一个维度都会对应一个状态参数,只有正确定义了状态参数,我们才能用决策来正确地进行状态转移。
最大子数组之和
除了回文子串问题以外,接下来,让我们来看一个求最大子数组之和的问题。
问题:给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入:[-2, 1, -3, 4, -1, 3, -5, 1, 2]
输出:6
解释:连续子数组 [4,-1, 3] 的和最大为 6。
算法问题分析
按照解题模板,先来确认 初始化状态。我们试着用回文子串中的方法来定义备忘录,即 $DP[i][j]$ 对应的值是起始位置为 $i$ 结束位置为 $j$ 构成的最大子的子数组和。
按照这个思路,那么原问题的答案应该存放在 $DP[0][n]$ 当中。但是这样设计备忘录,问题就复杂了。由于我们要求的只是一个最值,所有子问题最终要规约到从索引 0 到 n,因此没有必要同时记录子数组的起始和结束位置。
在这里我们对备忘录存储的状态进行简化,将 $DP[i][j]$ 简化成 $DP[i]$,其对应值表示的是 $nums[0…i]$ 中的最大子数组之和。 接着, 状态参数 就清晰明了,即 n。
我们再来看看如何进行 决策。由于动态规划的当前子问题需要由当前子问题的子问题 ➕ 当前决策来决定,同时,这又是一个求最值的动态规划问题(请你尝试使用之前讲到的方法来判断一下这个问题是不是动归问题)。
因此,我们要决策的就是是否要将当前子问题中额外的数字放入整个计算当中,以获得“更大”的子数组之和:
- 如果放入额外的数字,得到状态A;
- 如果不让入额外的数字,得到状态B。
综上所述,我们可以得到经过决策的状态转移,即 max(状态A, 状态B)。现在,我们是不是可以开始写状态转移方程了?
等一下,在写之前我们再多思考几秒钟。假设我们知道了 $DP[i-1]$,我们真的可以推导出 $DP[i]$ 吗?如果按照这样的备忘录定义($DP[i]$ 是 $nums[0…i]$ 中的最大子数组之和)是不能的。我根据示例中的输入画出了下面这张图,你看一下就明白了。
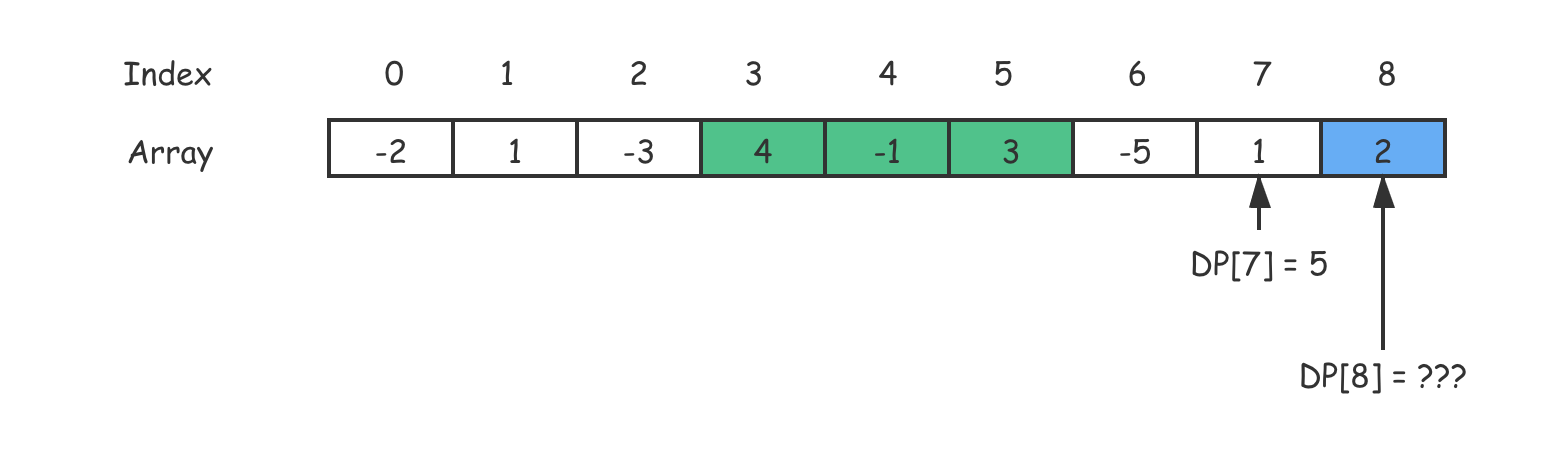
仔细想一下,子问题 $DP[8]$ 是不能根据子问题 $DP[7]$ ➕ 决策推导出来的。这是因为在子数组问题中有一个强加属性,即子数组要连续。
按照之前的备忘录定义,并不能保证 $nums[0…i-1]$ 中的最大子数组与 $nums[i]$ 是连续的(在示例中,$i = 6$ 的位置的 -5 就是一个极大的副作用),也就没办法从 $DP[i-1]$ 推导出 $DP[i]$了。
所以说这样的备忘录定义是错误的,无法得到合适的状态转移方程。
写出状态转移方程
对于这类子数组问题,我们需要重新定义备忘录的含义,即 $DP[i]$ 表示的是以 $i$ 为结束位置的最大子数组之和。
这样一来,以结束位置作为导向,就一定能跟后续子问题相连。现在,我们可以写出状态转移方程了。
\[DP(i, j)=\\left\\{\\begin{array}{c} 0, i = 0\\\\ DP\[i\] = max(nums\[i\], nums\[i\]+dp\[i-1\]), i > 0 \\end{array}\\right.\]编写代码进行求解
我直接给出代码,然后再做解释。
Java 实现:
int maxSubArray(int[] nums) {
int n = nums.length; if (0 == n) return 0;
int[] dp = new int[n];
for (int i = 0; i < n; i++) dp[i] = Integer.MIN_VALUE; // 初始化状态
dp[0] = nums[0];
int res = dp[0];
for (int i = 1; i < n; i++) {
dp[i] = Math.max(nums[i], dp[i-1] + nums[i]);
res = Math.max(res, dp[i]);
}
return res;
}
C++ 实现:
int MaxSubArray(vector<int>& nums) {
int n = nums.size(); if (0 == n) return 0;
int dp[n];
for (int i = 0; i < n; i++) dp[i] = INT_MIN; // 初始化状态
dp[0] = nums[0];
int res = dp[0];
for (int i = 1; i < n; i++) {
dp[i] = max(nums[i], dp[i-1] + nums[i]);
res = max(res, dp[i]);
}
return res;
}
代码的第 1 行中,我们首先处理了边界情况。如果数组长度为0,不包含任何元素,那么结果肯定为0。
接着,定义了备忘录数组dp,并通过循环将数组的值全部初始化为 INT_MIN,这样就能确保每次求出来的有效值可以直接当作最大值使用。然后,我们令 $dp[0]$ 为 $nums[0]$,也就是以 0 这个位置结尾的数组,其最大子数组之和就是dp的第 1 个元素。
到了算法的主要计算部分,我们不断遍历整个数组。每次遍历时,首先确定是需要开始一个新的连续子数组,还是扩展之前的连续子数组。如果当前位置的元素大于前面最优解子数组与当前元素之和,说明应该以当前位置开始一个新的子数组;否则说明当前元素应该是前一个最优解的扩展,得到一个更大的连续子数组。
接着,我们将当前连续子数组的和与之前遍历过程中保存的最大子数组之和进行比较,如果更大则替换掉之前保存的结果,这说明相对于之前保存的结果,我们遇到了求和更大的一个子串;否则说明当前子串之和小于之前找到过的最大值,因此依然保留之前的结果。
最后我们返回存储的最大值即可。这也就是我们整个数组的最大连续子数组之和。
空间复杂度优化
由于这个问题不太复杂,其实你可以使用暴力法求出,不过那样做效率还是太低,且不会得到面试官的认同。以上解法的时间复杂度为 O(N),空间复杂度为 O(N),相较暴力解法的 O(n2) 来说已经很优秀了。
那么现在,如果面试官问你是否还有优化的余地,你会从哪个角度下手呢?根据前面的分析,我们知道 $DP[i]$ 仅和 $DP[i-1]$ 的状态有关,因此可以进行状态压缩,即降低备忘录的空间复杂度。
我们无需保存一个长度为 n 的数组来存储状态,只需要两个整数型变量就够了。
Java 实现:
int maxSubArrayAdvanced(int[] nums) {
int n = nums.length; if (0 == n) return 0;
int dp_0 = nums[0], dp_1 = 0; // 初始化状态
int res = dp_0;
for (int i = 1; i < n; i++) {
dp_1 = Math.max(nums[i], dp_0 + nums[i]);
dp_0 = dp_1;
res = Math.max(res, dp_1);
}
return res;
}
C++ 实现:
int MaxSubArrayAdvanced(vector<int>& nums) {
int n = nums.size(); if (0 == n) return 0;
int dp_0 = nums[0], dp_1 = 0; // 初始化状态
int res = dp_0;
for (int i = 1; i < n; i++) {
dp_1 = max(nums[i], dp_0 + nums[i]);
dp_0 = dp_1;
res = max(res, dp_1);
}
return res;
}
这样一来,我们就完美地解决了最大子数组之和这个动态规划问题。从这个问题可以看出,备忘录的定义十分重要。
在这个题目中,我们需要将 $DP[i]$ 定义为以 $i$ 结尾的子问题答案,因为只有这样才能建立起 $DP[i]$ 与 $DP[i-1]$ 之间的关系,通过决策写出状态转移方程。
课程总结
所谓动态规划的子数组问题,就是从一个数组中寻找满足条件,并可以得到最优结果的一个最长的子数组序列的问题。
在设计备忘录时,我们根据实际情况缩减了问题中的状态数量,虽然缩减的方法不是非常套路,但是因为大多数缩减状态的方法大同小异,所以你可以根据这种思路去思考如何对类似问题的状态数量进行控制。状态数量会直接影响问题的空间复杂度和时间复杂度,状态越少,空间和时间复杂度肯定也就越小,求解方法也就越优秀。
最后,我们还讲解了如何在状态数量不变的情况下,根据状态的依赖关系,进一步缩减备忘录的空间,进一步降低空间复杂度。
由于实际的动态规划问题的状态数量肯定比较大,会带来较多的空间消耗。因此,在解决实际问题的时候,这种缩减备忘录空间的做法是非常常见的,我们有必要学习和掌握。
我们通过本课的两个子数组问题,认识了子数组这类动态规划问题的形式,了解了如何寻找状态和子问题、构建状态转移方程,并对其进行优化。在后续的课程中,你还会看到更复杂的子数组问题。到时候,希望你能够利用这节课所学到的内容,做到举一反三,百尺竿头更进一步。
课后思考
事实上,子串问题在很多情况下是可以使用滑动窗口来解决的。那对于子数组问题来说,我们该如何区分是该使用滑动窗口等传统算法来解决,还是该用动态规划来解决呢?请你给出能使用滑动窗口解决的子数组问题,并比较它与动态规划问题之间的区别。
不知道你今天的收获如何呢?如果感觉已经掌握了解题思路,不妨也去考考你的同事或者朋友吧,刚好也有机会复述一遍今天所学。