dynamic-programming-course
07|完全背包:深入理解背包问题
你好,我是卢誉声。
在上节课中,我们用动态规划解法,成功解决了动态规划领域中的 Hello World 问题。这个问题虽然比较初级,但却很有代表性,它比较全面地展示了动归解题的套路。
但光解决一个0-1背包问题显然不够过瘾。如果你觉得应用动态规划的解题套路还不太熟练,没关系。现在我们就趁热打铁,继续刨根问底,讨论背包问题。
首当其冲的就是完全背包问题。它仍然是动态规划领域的经典问题,但是比0-1背包问题要复杂一些。不过嘛,我们之前总结的解题套路还是比较具有普适性的,因此我们仍然可以将其套用在完全背包问题上。
在开始今天的课程前,请你思考这样一个问题: 既然都是背包问题,那么完全背包跟0-1背包问题会如何影响状态转移方程呢?
你不妨带着这个问题,有针对性地学习今天的内容。
完全背包问题
我们先来看看完全背包问题的描述。
问题:给你一个可放总重量为 $W$ 的背包和 $N$ 个物品,对每个物品,有重量 $w$ 和价值 $v$ 两个属性,那么第 $i$ 个物品的重量为 $w[i]$,价值为 $v[i]$。现在让你用这个背包装物品,每种物品都可以选择任意多个,问这个背包最多能装的价值是多少?
示例:
示例:
输入:W = 5, N = 3
w = [3, 2, 1], v = [5, 2, 3]
输出:15
解释:当 i = 2 时,选取 5 次,总价值为 5 * 3 = 15。
问题描述还是这么简单,如果你回过头,去看上一课的0-1背包的问题描述,你会发现,完全背包问题只在原来的基础上多加了一句话,那就是:“每种物品都可以选择任意多个”。除此之外,完全相同。
可不要小看这一句话,它的出现让我们的问题复杂度上了一个台阶。
算法问题分析
不同于0-1背包问题(每件物品只能拿一次),在完全背包问题中,每件物品可以拿任意多件,只要背包装得下就行。
如果从每件物品的角度来看,与之相关的决策已经不再是选拿(1)或者不拿(0)了;而是拿 0 件、拿 1 件、拿 2 件……直到拿到 ($W / w[i]$) 件物品为止。
我曾在上一课中对0-1背包问题做了较为全面的分析,最后得出的结论就是,它是一个动态规划问题。那么为了起到对照的作用,我在这里再次给出分析步骤,不过比之前的稍微简化一些。
首先,题设中出现了“最多能装的价值是多少”这样的论断。既然有“最”字,那么我们需要先考虑贪心算法,这里我直接给出一个反例:按照示例中的提示,虽然 $i = 1$ 的物品价值最高,但最后得到的解不是真正的答案。
因此,为了获得整体最优解,我们需要考虑穷举。为了高效地进行穷举操作,我们需要考虑使用动态规划来解。仿照上一课的做法,我们对该问题做一个分析,看看它是否满足求解动态规划的特征。
- 重叠子问题:在穷举的过程中肯定存在重复计算的问题。这是因为各种排列组合间肯定存在重叠子问题的情况;
- 无后效性:选择了一个物品后,背包还能容纳的重量与总价值是确定的,后续选择的物品(即便重复选择相同的物品)不会对当前这个选择产生副作用。因此,该问题无后效性;
- 最优子结构:在选定了一个物品后,继续做决策时,我们是可以使用之前计算的重量和价值,也就是说后续的计算可以通过前面的状态推导出来。因此,该问题存在最优子结构。
这个分析算法问题的方法特别有效,希望你能够养成这个基本分析的习惯。这样一来,你不仅能少走弯路,而且能有目的性地解决面试问题。
写出状态转移方程
既然我们已经确定了这是个动态规划问题,那么就拿出我们的法宝:动态规划解题框架。现在,就让我们沿着解题框架的顺序,来写出状态转移方程。
首先,我们先来确定动态规划解法当中的最初子问题,即 初始化状态。这跟0-1背包问题有些类似:由于物品的数量没有限制,因此只有当背包的容量为 0 时要终止执行,但如果压根儿就没有物品可选,那么自然背包的重量也为 0。如果体现在代码上,就是当没有物品时重量为 0;而重量为 0 时显然物品数量也为 0。
接着,我们来确定动态规划问题中的 状态参数,这与0-1背包问题几乎一样:
- 背包内物品的数量 $N$ 在增加,它是一个变量;
- 同时,背包还能装下的重量 $W$ 在减少,它也是一个变量。
因此,当前背包内的物品数量 $N$ 和背包还能装下的重量 $W$ 就是这个动态规划问题的状态参数。
然后,我们再来看如何进行 决策。这里的区别,跟0-1背包问题中的决策差别就比较大了。由于每种物品的数量是无限制的,因此就像前面给出的示例那样,我们可以将同一种物品多次放入背包。
因此,对于第 $tn$ 种物品,我们有 k 种选择(其中 0 ≤ k * $w[tn]$ ≤ W):我们可以从 0 开始,拿第 0 件、第 1 件、第 2 件……直到第 ($W / w[tn]$) 件物品为止。然后在这么多子问题下,选择最优的那一种情况。
所以,我们可以看出,完全背包问题决策的核心在于,针对一种物品,它需要考察拿不同数量的情况下的最优解。这显然与0-1背包问题的决策完全不同,总结来说就是:
- 0-1背包问题:针对当前物品,是放入背包,还是不放入背包时的价值最大;
- 完全背包问题:针对当前物品,应放入多少件当前物品,价值最大。
最后,动态规划是需要一个 备忘录 来加速算法的。由于有两个状态参数,因此我们考虑使用二维数组来存储子问题的答案。跟之前一样,为了通用起见,我将其命名为 $DP[tn][rw]$,它的含义是:背包容量还剩 $rw$ 时,放入前 $tn$ 种物品时的最大价值。
由于这个问题跟0-1背包问题有些相似,因此今天我们做一个新的尝试,那就是在不写出递归代码的情况下,直接根据上面的信息写出状态转移方程。它是这样的:
\[DP(tn, rw)=\\left\\{\\begin{array}{c} 0, tn<=0\\\\ 0, rw<=0\\\\ DP(tn-1,rw), rw<w\[tn\]\\\\ max\\{ DP(tn-1,rw-k\*w\[tn\])+k\*v\[tn\] \\},(0\\leqq k \\leqq rw) \\end{array}\\right.\]我们有了完整的状态转移方程,就可以开始编写代码了。
编写代码进行求解
现在,所有的先决条件都解决了,因此我直接给出以下代码,你可以参考一下。
Java 实现:
int bag(int[] w, int[] v, int N, int W) {
// 创建备忘录
int[][] dp = new int[N+1][W+1];
// 初始化状态
for (int i = 0; i < N + 1; i++) { dp[i][0] = 0; }
for (int j = 0; j < W + 1; j++) { dp[0][j] = 0; }
// 遍历每一件物品
for (int tn = 1; tn < N + 1; tn++) {
// 背包容量有多大就还要计算多少次
for (int rw = 1; rw < W + 1; rw++) {
dp[tn][rw] = dp[tn-1][rw];
// 根据rw尝试放入多次物品,从中找出最大值,作为当前子问题的最优解
for (int k = 0; k <= rw / w[tn]; k++) {
dp[tn][rw] = Math.max(dp[tn][rw], dp[tn-1][rw-k*w[tn]] + k*v[tn]);
}
}
}
return dp[N][W];
}
int solveBag() {
int N = 3, W = 5; // 物品的总数,背包能容纳的总重量
int[] w = {0, 3, 2, 1}; // 物品的重量
int[] v = {0, 5, 2, 3}; // 物品的价值
return bag(w, v, N, W); // 输出答案
}
C++ 实现:
int DP(const std::vector<int>& w, const std::vector<int>& v, int N, int W) {
int dp[N+1][W+1]; // 创建备忘录
memset(dp, 0, sizeof(dp));
// 初始化状态
for (int i = 0; i < N + 1; i++) { dp[i][0] = 0; }
for (int j = 0; j < W + 1; j++) { dp[0][j] = 0; }
// 遍历每一件物品
for (int tn = 1; tn < N + 1; tn++) {
// 背包容量有多大就还要计算多少次
for (int rw = 1; rw < W + 1; rw++) {
dp[tn][rw] = dp[tn-1][rw];
// 根据rw尝试放入多次物品,从中找出最大值,作为当前子问题的最优解
for (int k = 0; k <= rw / w[tn]; k++) {
dp[tn][rw] = max(dp[tn][rw], dp[tn-1][rw-k*w[tn]] + k*v[tn]);
}
}
}
return dp[N][W];
}
int DPSol() {
int N = 3, W = 5; // 物品的总数,背包能容纳的总重量
std::vector<int> w = {0, 3, 2, 1}; // 物品的重量
std::vector<int> v = {0, 5, 2, 3}; // 物品的价值
return DP(w, v, N, W); // 输出答案
}
时间复杂度优化
如果我们认真分析上面的代码,就可以发现代码中使用了三重循环:
- 首先是遍历物品;
- 然后是遍历剩余容量;
- 最后是遍历物品数量。
那么这个解法的算法时间复杂度是多少呢?如果我们假定物品数量是 k,容量是 v,那么最后的时间复杂度就是 O(kv2)。
我们如果回顾一下0-1背包问题,就会发现0-1背包的时间复杂度是 O(kv)。虽然完全背包问题比0-1背包问题更复杂一些,但是,出现指数级别的复杂度可不是一件好事。我们得比一般人做得更好。那么,我们能够通过某种方式降低完全背包的时间复杂度吗?
在回答这个问题前,我们来进行一些简单的探讨。
为何时间复杂度会增加?
现在,按照题设和上面的状态转移方程的定义,我们来思考一下:假如要拿第 $tn $个物品,当前物品重量为 $w[tn]$,我们会考察放入第 0 件、第 1 件、第 2 件…… k 件该物品时的价值,并取最大值。
因此,要求剩余容量为 $rw$ (即 $rw$ - 0*$w[tn]$ )时的最优解,就需要遍历求出 $rw$ - 0*$w[tn]$、$rw$ - 1*$w[tn]$、$rw$ - 2*$w[tn]$ … $rw$ - k*$w[tn]$,然后在其中挑出最大的那个,作为当前子问题的解。这导致了算法执行时多了一层循环。
让我们仔细考虑一下这个求解过程,如果我们求解剩余容量为 $rw$ - 1*$w[tn]$ 时的最优解,就需要遍历求出 $rw$ - 1*$w[tn]$、$rw$ - 2*$w[tn]$ … $rw$ - k*$w[tn]$,因此我们肯定会再次求解 $rw$ - 2*$w[tn]$。所以,在完全背包问题中,依然存在重复计算。
针对这一问题,我们是否可以避免这个重复计算呢?答案是肯定的。至于方法其实很简单,我们只需要把问题转换成一种新的0-1背包问题就行了。
改进状态转移方程
回忆一下,在0-1背包问题中,当我们求第 $tn$ 个物品的最优解时,是从“放入该物品”和“不放入该物品”两种情况中作出决策的。也就是说,第 $tn$ 个物品状态下的最优解,是第 $tn - 1$ 个物品的最优解(子问题) ➕ 当前的决策推导出来的。
0-1背包问题解决方案的关键在于,当剩余容量 $rw$ 确定,处理第 $tn$ 件物品的时候,我们只需要考虑拿或不拿第 $tn$ 件物品,而不需要考虑放入几个第 $tn$ 件物品。
根据上述思路,在解决完全背包问题时,我们可以把之前的重叠子问题等价地转化成一个新的重叠子问题来解决,以消除上面提到的重复计算(多出来的那个子循环)。另 $rw$ 确定时,在处理第 $tn$ 件物品的时候,也只需要考虑拿或不拿第 $tn$ 件物品。怎么做呢?我们只需要从以下两种情况里作出决策:
- 不拿第 $tn$ 个物品,那么价值就是 $DP[tn-1][rw]$(状态 A);
- 拿第 $tn$ 个物品,那么价值就是 $DP[tn][rw-w[tn]] + v[tn]$(状态 B)。
在剩余容量为 $rw$ 的时候,其最大价值就是 max(状态 A, 状态 B)。也就是说,此时处理第 $tn$ 件物品的最优解,就是从上面两个状态的结果中取最大值。
因此,每一次我们只需考虑,当前是否要把第 $tn$ 个物品放入背包就行了。至于之前有没有放过第 $tn$ 件物品,以及放了几件进入背包,已经在容量更小的时候计算过了(需要注意的是,动态规划的计算过程是自底向上的)。
如果你还是觉得有点晕,没关系,我们再换一种说法。在0-1背包问题里,因为一个物品只能放入一次,所以我们是以上一个物品的最优解为基础进行决策推导的。而在完全背包问题里,因为一个物品可以放入 0 到多次,所以我们必须以“当前物品 $tn$ 在容量更小时,计算出的最优解”为基础进行决策推导。
这样可以隐含一个过程:我们在当前物品 $tn$ 状态下,当容量 $rw$ 更小的时候,就已经选择过 0 到多次当前物品了,而且得到的最优解存储在缓存中,这部分不需要每次都重复求解。
通过以上分析,我们得到了优化后的状态转移方程:
\[DP(tn, rw)=\\left\\{\\begin{array}{c} 0, tn<=0\\\\ 0, rw<=0\\\\ DP(tn-1,rw), rw<w\[tn\]\\\\ max( DP(tn-1,rw),DP(tn,rw-w\[tn\])+v\[tn\] ) \\end{array}\\right.\]方程中,$tn$表示当前物品序号,$rw$表示目前背包剩余容量。$DP(tn,rw)$ 也就是在目前背包剩余$rw$容量的情况下,放入第$tn$个物品的最大价值。$w[tn]$就是第$tn$个物品的重量,$v[tn]$就是第$tn$个物品的价值。
改进代码的时间复杂度
接着,按照状态转移方程的指导,给出相应的算法代码。你可以参考以下代码,看看跟之前的解法有何不同。
Java 实现:
int bag(int[] w, int[] v, int N, int W) {
// 创建备忘录
int[][] dp = new int[N+1][W+1];
// 初始化状态
for (int i = 0; i < N + 1; i++) { dp[i][0] = 0; }
for (int j = 0; j < W + 1; j++) { dp[0][j] = 0; }
// 遍历每一件物品
for (int tn = 1; tn < N + 1; tn++) {
// 背包容量有多大就还要计算多少次
for (int rw = 1; rw < W + 1; rw++) {
dp[tn][rw] = dp[tn-1][rw];
// 如果可以放入,则尝试放入第tn件物品
if (w[tn] <= rw) {
dp[tn][rw] = Math.max(dp[tn][rw], dp[tn][rw-w[tn]] + v[tn]);
}
}
}
return dp[N][W];
}
int solveBag() {
int N = 3, W = 5; // 物品的总数,背包能容纳的总重量
int[] w = {0, 3, 2, 1}; // 物品的重量
int[] v = {0, 5, 2, 3}; // 物品的价值
return bag(w, v, N, W); // 输出答案
}
C++ 实现:
int DP(const std::vector<int>& w, const std::vector<int>& v, int N, int W) {
int dp[N+1][W+1]; // 创建备忘录
memset(dp, 0, sizeof(dp));
// 初始化状态
for (int i = 0; i < N + 1; i++) { dp[i][0] = 0; }
for (int j = 0; j < W + 1; j++) { dp[0][j] = 0; }
// 遍历每一件物品
for (int tn = 1; tn < N + 1; tn++) {
// 背包容量有多大就还要计算多少次
for (int rw = 1; rw < W + 1; rw++) {
dp[tn][rw] = dp[tn-1][rw];
// 如果可以放入,则尝试放入第tn件物品
if (w[tn] <= rw) {
dp[tn][rw] = max(dp[tn][rw], dp[tn][rw-w[tn]] + v[tn]);
}
}
}
return dp[N][W];
}
int DPSol() {
int N = 3, W = 5; // 物品的总数,背包能容纳的总重量
std::vector<int> w = {0, 3, 2, 1}; // 物品的重量
std::vector<int> v = {0, 5, 2, 3}; // 物品的价值
return DP(w, v, N, W); // 输出答案
}
我在下面的表格中,用箭头画出了容量为 5 时的求解路径。你可以参照这个求解路径来加深对代码的理解。
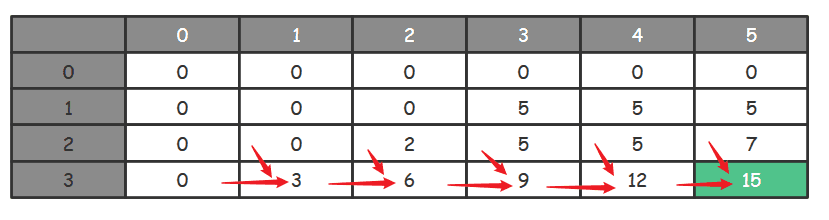
不知道你发现了没有,在改进后的代码中没有 k 参与计算了,那么这个由 0 到 k 的循环过程去哪了呢?其实,它隐含在了新的重叠子问题的计算过程中,这一过程可以用下图描述:
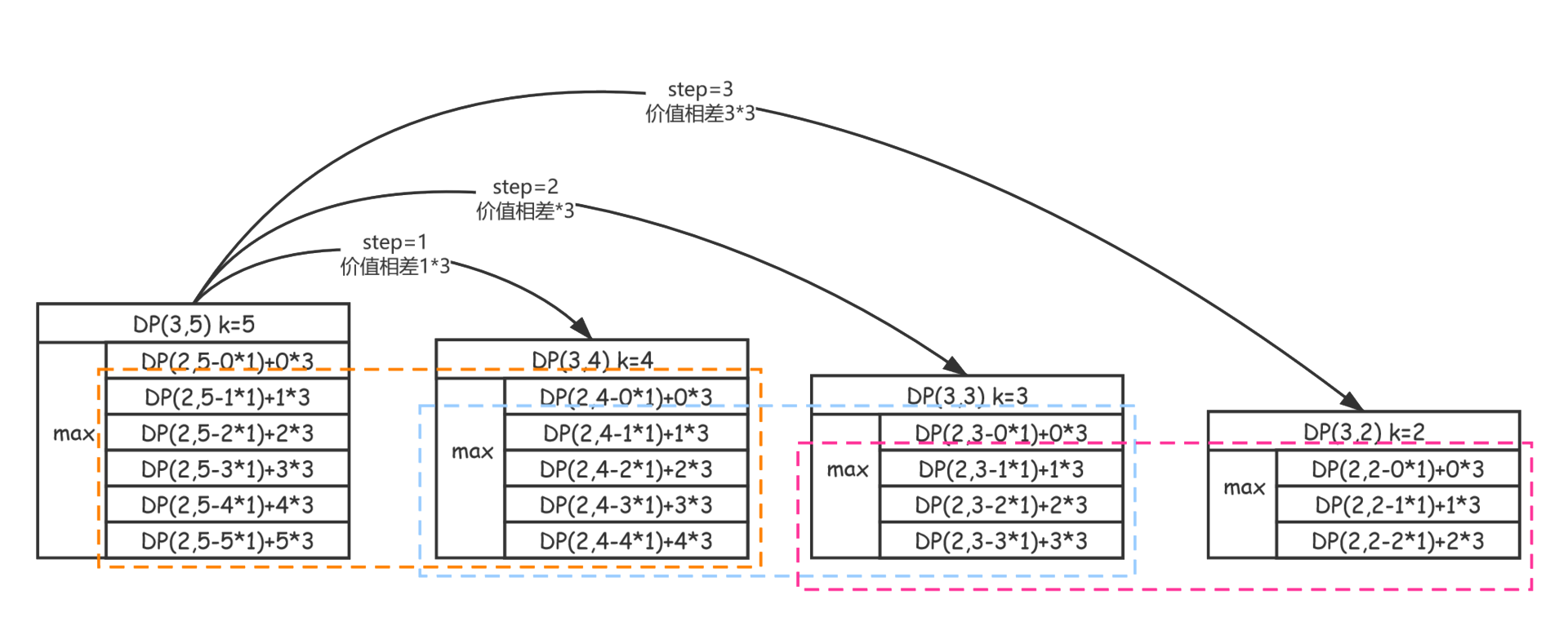
从图中我们可以看出,虚线框就是我们所说的会包含重叠子问题的部分内容(并非意味着虚线框里的内容是重叠子问题)。在计算$DP(3, 5)$时 $k = 5$,因此循环从 6 个值中求解最优解,这6个值就是$DP(2,5-0*1)+0*3$到$DP(2,5-5*1)+5*3$,也就是$DP(2,5 - k*1)+k*3$,此时背包剩余容量$rw$为5,第2件物品的重量为1,价值为3,所以$k$可以取0到5。我们只需要求出中的最大值即可。
但是我们可以看到其中的前五步所依赖的子问题,在 $DP(3, 4)$ 这个问题中也会被计算到,此时 $k = 4$,只不过在$k=5$的时候需要在$k=4$的求解基础上加上1个物品的价值。因此,$DP(3, 4)$ 和 $DP(3, 5)$ 之间只相差了这一步循环和1个物品的价值,但我们的确没必要把$DP(3,4)$中求解过的子问题在$DP(3,5)$中重复求解一遍,而是通过这种换算关系直接复用$DP(3,4)$的结果即可。
然后我们再看 $DP(3, 5)$ 和 $DP(3, 3)$ 两个子问题,前四步依赖的子问题是完全相同的(都相差2个物品的价值),因此这两个子问题之间(状态)只相差了两次循环步骤,然后再加上2个物品的价值。以此类推,原本方程中的 $k$ 次循环,其实是在其它子问题中被重复计算了。
空间复杂度优化
我们刚刚讲解了如何优化动归解法下完全背包问题的时间复杂度。现在,再让我们看看如何优化它的空间复杂度。
动态规划对内存要求高
还记得备忘录这个词吧,在我们解动态规划问题时,总会用到它。名字确实比较高端、上档次,但说白了,它无非就是一块事先开辟好的缓存区域。我们总是要对计算结果进行缓存,而缓存可以避免对结果进行重复计算。
但是,鱼与熊掌不可兼得,当状态数量非常多的时候,缓存的占用空间也会变得非常非常大。因此,如果我们要优化动态规划的空间复杂度,就必须想办法减少缓存的大小,毕竟其它的空间相对于缓存都是九牛一毛。
寻找优化空间复杂度的方法
我们先来回顾一下时间复杂度优化一节的状态转移方程:
\[DP(tn, rw)=\\left\\{\\begin{array}{c} 0, tn<=0\\\\ 0, rw<=0\\\\ DP(tn-1,rw), rw<w\[tn\]\\\\ max( DP(tn-1,rw),DP(tn,rw-w\[tn\])+v\[tn\] ) \\end{array}\\right.\]从状态转移方程中,我们可以知道:如果想求 $DP(tn, rw)$,那么我们只依赖于$DP(tn-1, rw)$和$DP(tn, 0)$。
如果从状态备忘录的角度上来说,就是我们只关心 $tn - 1$ 时的结果和 $tn$ 相同时的结果。也就是说,当前的计算只使用缓存中当前这一行和上一行的计算结果。
既然如此,我们就可以采用滚动数组的方式,定义一个只有两行的数组。
- 在计算第 1 个物品时,用第 0 行做 $tn - 1$ 的缓存,用第 1 行做 $tn$ 的缓存;
- 在计算第 2 个物品时,用第 1 行做 $tn - 1$ 的缓存,用第 0 行做 $tn$ 的缓存;
- 在计算第 3个物品时,用第 0 行做 $tn - 1$ 的缓存,而用第 1 行做 $tn$ 的缓存……以此类推。
这个过程,可以用下面的图展示出来。
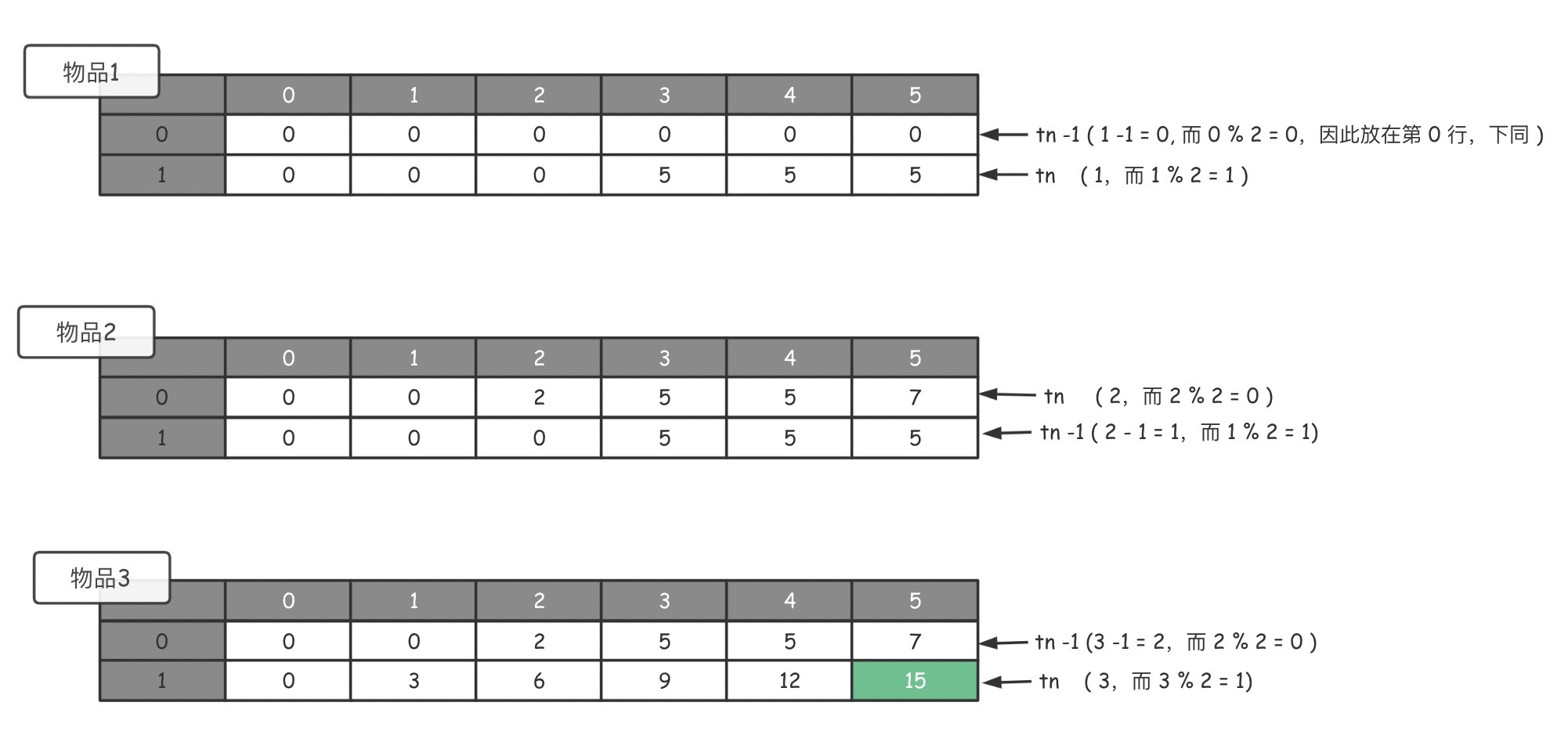
通过上述方法,我们把那张庞大的状态转移表,优化成了只有两行的数组。可以预见的是,无论输入的数据多么庞大,改进后的算法占用的空间都会十分稳定,妙哉!
改进代码的空间复杂度
现在,我们有了明确的优化思路,那就是用一个只有两行的数组来代替原来的状态转移表(即备忘录)。在这种情况下,状态转移方程不会有什么变化,我们只需要对代码中的备忘录稍作修改即可。
Java 实现:
int bag(int[] w, int[] v, int N, int W) {
// 创建备忘录
int[][] dp = new int[2][W+1];
// 初始化状态
for (int i = 0; i < 2; i++) { dp[i][0] = 0; }
for (int j = 0; j < W + 1; j++) { dp[0][j] = 0; }
// 遍历每一件物品
for (int tn = 1; tn < N + 1; tn++) {
// 背包容量有多大就还要计算多少次
for (int rw = 1; rw < W + 1; rw++) {
// tn % 2代表当前行的缓存索引
int ctn = tn % 2;
// 1 - ctn代表上一行的缓存索引
int ptn = 1 - ctn;
dp[ctn][rw] = dp[ptn][rw];
// 如果可以放入则尝试放入第tn件物品
if (w[tn] <= rw) {
dp[ctn][rw] = Math.max(dp[ctn][rw], dp[ctn][rw-w[tn]] + v[tn]);
}
}
}
return dp[N % 2][W];
}
int solveBag() {
int N = 3, W = 5; // 物品的总数,背包能容纳的总重量
int[] w = {0, 3, 2, 1}; // 物品的重量
int[] v = {0, 5, 2, 3}; // 物品的价值
return bag(w, v, N, W); // 输出答案
}
C++ 实现:
int DP(const std::vector<int>& w, const std::vector<int>& v, int N, int W) {
int dp[2][W+1]; // 创建备忘录
memset(dp, 0, sizeof(dp));
// 初始化状态
for (int i = 0; i < 2; i++) { dp[i][0] = 0; }
for (int j = 0; j < W + 1; j++) { dp[0][j] = 0; }
// 遍历每一件物品
for (int tn = 1; tn < N + 1; tn++) {
// 背包容量有多大就还要计算多少次
for (int rw = 1; rw < W + 1; rw++) {
// tn % 2代表当前行的缓存索引
int ctn = tn % 2;
// tn % 1代表上一行的缓存索引
int ptn = tn % 1;
dp[ctn][rw] = dp[ptn][rw];
// 如果可以放入则尝试放入第tn件物品
if (w[tn] <= rw) {
dp[ctn][rw] = max(dp[ctn][rw], dp[ctn][rw-w[tn]] + v[tn]);
}
}
}
return dp[N % 2][W];
}
int DPSol() {
int N = 3, W = 5; // 物品的总数,背包能容纳的总重量
std::vector<int> w = {0, 3, 2, 1}; // 物品的重量
std::vector<int> v = {0, 5, 2, 3}; // 物品的价值
return DP(w, v, N, W); // 输出答案
}
从代码中,我们可以看到,其唯一变化的就是缓存的定义和使用方法。
我们将缓存定义成只有 2 行。在使用的时候,我们利用求余的操作控制到底哪一行是当前行,哪一行是上一行,交替使用两部分缓存。通过这个巧妙的方式,我们大幅减少了缓存空间的使用,尤其在物品数量很多的时候效果会非常好。
至此,我们较为完美地解决了整个完全背包问题,无论是从时间复杂度,还是从空间复杂度角度上看,这段代码都称得上是 a master piece~
虽然完全背包问题已经在之前的0-1背包问题上复杂了许多,不过,关于背包的故事还没有结束。我会在后续的课程中,结合完全背包的衍生面试问题与你进行探讨。不过,你还是要把本节课中提到的技巧和方法多加练习一下,就目前来说这更为重要。
课程总结
让我们回到本课开篇的那个问题上来: 完全背包会如何影响状态转移方程呢?
显然,完全背包把问题复杂化了,曾经的我们,只需要决策当前物品放还是不放;但现在,我们需要考虑当前物品到底要放几个,才能到达最后的最优解。
从状态转移方程的角度上看,在原有0-1背包问题的基础上,它多了一层循环遍历。我们要通过这个循环找到一个答案:那就是到底该拿多少件当前物品。因此,上述问题的结论就是, 完全背包问题让状态转移方程多了一层循环迭代。
如果你已经理解到这个层面,那么恭喜你,面试这一关你已经达标了,面试官应该会很满意。因为根据我的经验,真就是有很多面试者会栽在这一类动归问题的复杂度上,更别提写出代码了。
但我们追求的不仅是弄懂,还要弄通。因为只有弄通了,才能解决咱们后续课程的动态规划问题。因此,我们还要考虑,如何从时间复杂度和空间复杂度上来进一步优化算法。
- 优化算法的时间复杂度:动态规划的重叠子问题并不一定是唯一的,不同的重叠子问题可能会带来不同的计算消耗。因此,我们要尽量将问题转换成时间复杂度最低的重叠子问题;
- 优化算法的空间复杂度:动态规划的核心在于状态存储(即备忘录),而状态存储必定带来消耗,也就是以空间换时间。但是在实际应用中,实际的存储条件并不一定能满足动态规划的标准状态存储方式。此时,我们要考虑如何压缩状态存储数,降低空间复杂度。
课后思考
我们已经学习了0-1背包和完全背包问题。特别的,在完全背包问题中,每一种物品的数量是无限的。现在,给你这样一个问题,如果每种物品不像0-1背包问题中那样只有一个,也不像完全背包问题中那样无限制,即每种物品有个数的限制(≥ 1)。那么在这种题设下,该如何使用动态规划来化解此问题呢?
在解决问题后,你是否能找到降低时间复杂度和空间复杂度的方法呢?
十分期待你的答案,欢迎你在留言区中与我交流!如果乍一看感觉解决不了,不妨再次复习下这节课的内容,或者考考你身边的同事或朋友呀。