data-structure-course
32 | 字符串匹配基础(上):如何借助哈希算法实现高效字符串匹配?
从今天开始,我们来学习字符串匹配算法。字符串匹配这样一个功能,我想对于任何一个开发工程师来说,应该都不会陌生。我们用的最多的就是编程语言提供的字符串查找函数,比如Java中的indexOf(),Python中的find()函数等,它们底层就是依赖接下来要讲的字符串匹配算法。
字符串匹配算法很多,我会分四节来讲解。今天我会讲两种比较简单的、好理解的,它们分别是:BF算法和RK算法。下一节,我会讲两种比较难理解、但更加高效的,它们是:BM算法和KMP算法。
这两节讲的都是单模式串匹配的算法,也就是一个串跟一个串进行匹配。第三节、第四节,我会讲两种多模式串匹配算法,也就是在一个串中同时查找多个串,它们分别是Trie树和AC自动机。
今天讲的两个算法中,RK算法是BF算法的改进,它巧妙借助了我们前面讲过的哈希算法,让匹配的效率有了很大的提升。那 RK算法是如何借助哈希算法来实现高效字符串匹配的呢?你可以带着这个问题,来学习今天的内容。
BF算法
BF算法中的BF是Brute Force的缩写,中文叫作暴力匹配算法,也叫朴素匹配算法。从名字可以看出,这种算法的字符串匹配方式很“暴力”,当然也就会比较简单、好懂,但相应的性能也不高。
在开始讲解这个算法之前,我先定义两个概念,方便我后面讲解。它们分别是 主串 和 模式串。这俩概念很好理解,我举个例子你就懂了。
比方说,我们在字符串A中查找字符串B,那字符串A就是主串,字符串B就是模式串。我们把主串的长度记作n,模式串的长度记作m。因为我们是在主串中查找模式串,所以n>m。
作为最简单、最暴力的字符串匹配算法,BF算法的思想可以用一句话来概括,那就是, 我们在主串中,检查起始位置分别是0、1、2….n-m且长度为m的n-m+1个子串,看有没有跟模式串匹配的。我举一个例子给你看看,你应该可以理解得更清楚。
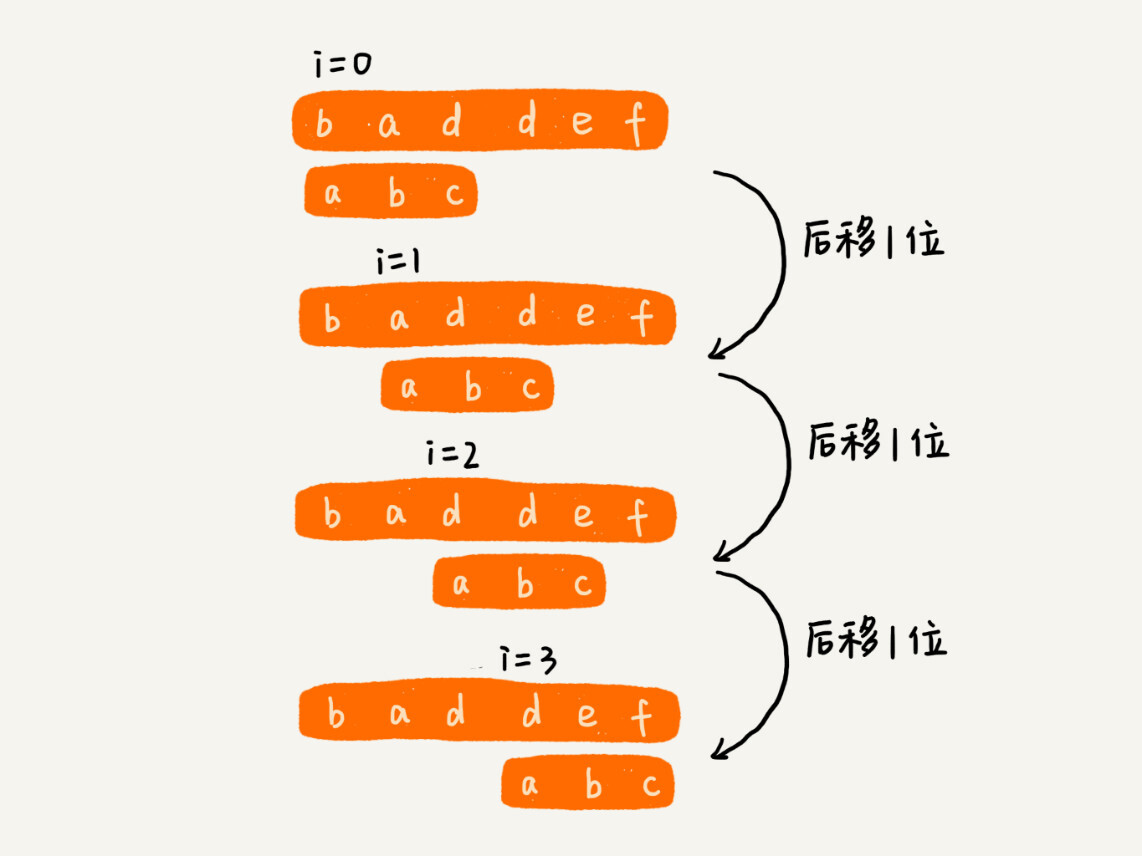
从上面的算法思想和例子,我们可以看出,在极端情况下,比如主串是“aaaaa….aaaaaa”(省略号表示有很多重复的字符a),模式串是“aaaaab”。我们每次都比对m个字符,要比对n-m+1次,所以,这种算法的最坏情况时间复杂度是O(n*m)。
尽管理论上,BF算法的时间复杂度很高,是O(n*m),但在实际的开发中,它却是一个比较常用的字符串匹配算法。为什么这么说呢?原因有两点。
第一,实际的软件开发中,大部分情况下,模式串和主串的长度都不会太长。而且每次模式串与主串中的子串匹配的时候,当中途遇到不能匹配的字符的时候,就可以就停止了,不需要把m个字符都比对一下。所以,尽管理论上的最坏情况时间复杂度是O(n*m),但是,统计意义上,大部分情况下,算法执行效率要比这个高很多。
第二,朴素字符串匹配算法思想简单,代码实现也非常简单。简单意味着不容易出错,如果有bug也容易暴露和修复。在工程中,在满足性能要求的前提下,简单是首选。这也是我们常说的 KISS(Keep it Simple and Stupid)设计原则。
所以,在实际的软件开发中,绝大部分情况下,朴素的字符串匹配算法就够用了。
RK算法
RK算法的全称叫Rabin-Karp算法,是由它的两位发明者Rabin和Karp的名字来命名的。这个算法理解起来也不是很难。我个人觉得,它其实就是刚刚讲的BF算法的升级版。
我在讲BF算法的时候讲过,如果模式串长度为m,主串长度为n,那在主串中,就会有n-m+1个长度为m的子串,我们只需要暴力地对比这n-m+1个子串与模式串,就可以找出主串与模式串匹配的子串。
但是,每次检查主串与子串是否匹配,需要依次比对每个字符,所以BF算法的时间复杂度就比较高,是O(n*m)。我们对朴素的字符串匹配算法稍加改造,引入哈希算法,时间复杂度立刻就会降低。
RK算法的思路是这样的:我们通过哈希算法对主串中的n-m+1个子串分别求哈希值,然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等,那就说明对应的子串和模式串匹配了(这里先不考虑哈希冲突的问题,后面我们会讲到)。因为哈希值是一个数字,数字之间比较是否相等是非常快速的,所以模式串和子串比较的效率就提高了。

不过,通过哈希算法计算子串的哈希值的时候,我们需要遍历子串中的每个字符。尽管模式串与子串比较的效率提高了,但是,算法整体的效率并没有提高。有没有方法可以提高哈希算法计算子串哈希值的效率呢?
这就需要哈希算法设计的非常有技巧了。我们假设要匹配的字符串的字符集中只包含K个字符,我们可以用一个K进制数来表示一个子串,这个K进制数转化成十进制数,作为子串的哈希值。表述起来有点抽象,我举了一个例子,看完你应该就能懂了。
比如要处理的字符串只包含a~z这26个小写字母,那我们就用二十六进制来表示一个字符串。我们把a~z这26个字符映射到0~25这26个数字,a就表示0,b就表示1,以此类推,z表示25。
在十进制的表示法中,一个数字的值是通过下面的方式计算出来的。对应到二十六进制,一个包含a到z这26个字符的字符串,计算哈希的时候,我们只需要把进位从10改成26就可以。
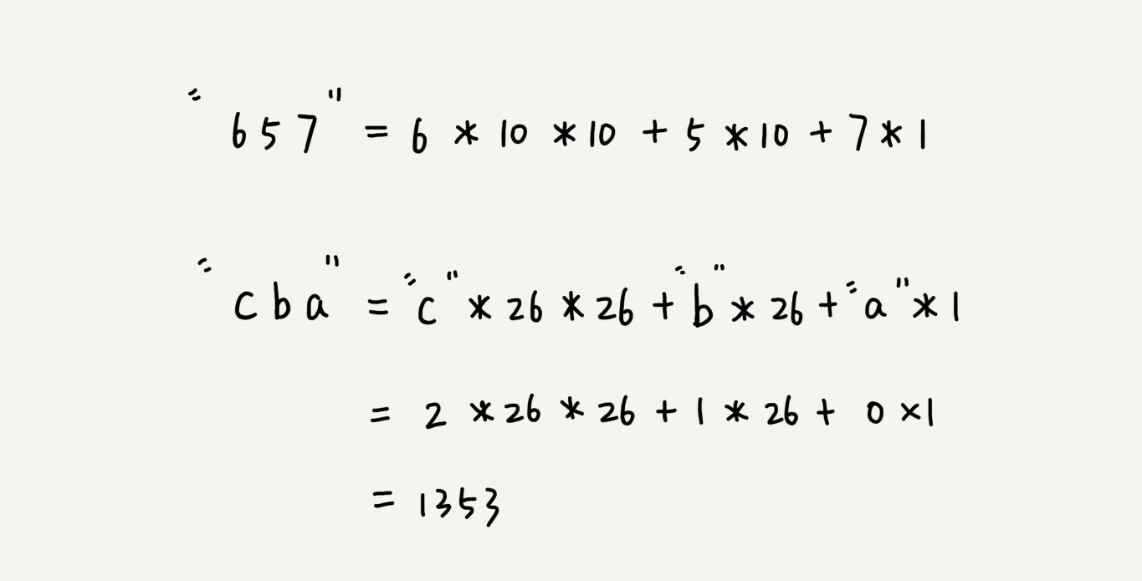
这个哈希算法你应该看懂了吧?现在,为了方便解释,在下面的讲解中,我假设字符串中只包含a~z这26个小写字符,我们用二十六进制来表示一个字符串,对应的哈希值就是二十六进制数转化成十进制的结果。
这种哈希算法有一个特点,在主串中,相邻两个子串的哈希值的计算公式有一定关系。我这有个例子,你先找一下规律,再来看我后面的讲解。
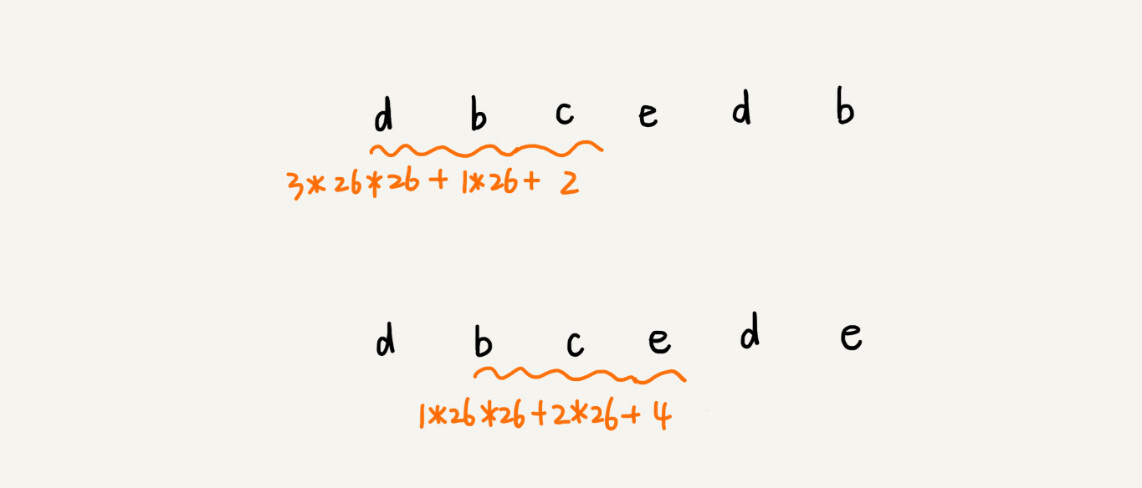
从这里例子中,我们很容易就能得出这样的规律:相邻两个子串s[i-1]和s[i](i表示子串在主串中的起始位置,子串的长度都为m),对应的哈希值计算公式有交集,也就是说,我们可以使用s[i-1]的哈希值很快的计算出s[i]的哈希值。如果用公式表示的话,就是下面这个样子:

不过,这里有一个小细节需要注意,那就是26^(m-1)这部分的计算,我们可以通过查表的方法来提高效率。我们事先计算好26^0、26^1、26^2……26^(m-1),并且存储在一个长度为m的数组中,公式中的“次方”就对应数组的下标。当我们需要计算26的x次方的时候,就可以从数组的下标为x的位置取值,直接使用,省去了计算的时间。
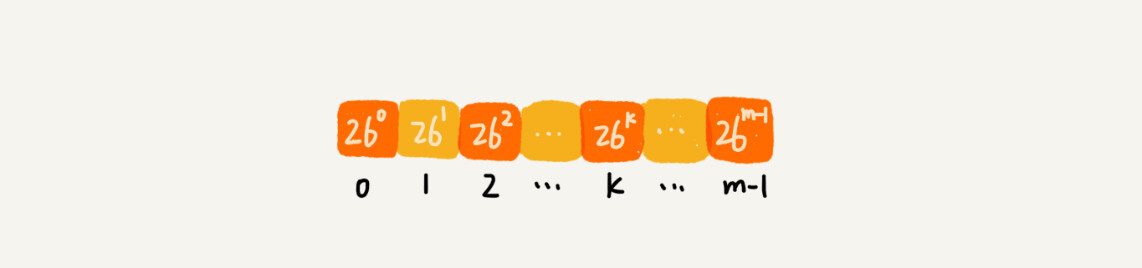
我们开头的时候提过,RK算法的效率要比BF算法高,现在,我们就来分析一下,RK算法的时间复杂度到底是多少呢?
整个RK算法包含两部分,计算子串哈希值和模式串哈希值与子串哈希值之间的比较。第一部分,我们前面也分析了,可以通过设计特殊的哈希算法,只需要扫描一遍主串就能计算出所有子串的哈希值了,所以这部分的时间复杂度是O(n)。
模式串哈希值与每个子串哈希值之间的比较的时间复杂度是O(1),总共需要比较n-m+1个子串的哈希值,所以,这部分的时间复杂度也是O(n)。所以,RK算法整体的时间复杂度就是O(n)。
这里还有一个问题就是,模式串很长,相应的主串中的子串也会很长,通过上面的哈希算法计算得到的哈希值就可能很大,如果超过了计算机中整型数据可以表示的范围,那该如何解决呢?
刚刚我们设计的哈希算法是没有散列冲突的,也就是说,一个字符串与一个二十六进制数一一对应,不同的字符串的哈希值肯定不一样。因为我们是基于进制来表示一个字符串的,你可以类比成十进制、十六进制来思考一下。实际上,我们为了能将哈希值落在整型数据范围内,可以牺牲一下,允许哈希冲突。这个时候哈希算法该如何设计呢?
哈希算法的设计方法有很多,我举一个例子说明一下。假设字符串中只包含a~z这26个英文字母,那我们每个字母对应一个数字,比如a对应1,b对应2,以此类推,z对应26。我们可以把字符串中每个字母对应的数字相加,最后得到的和作为哈希值。这种哈希算法产生的哈希值的数据范围就相对要小很多了。
不过,你也应该发现,这种哈希算法的哈希冲突概率也是挺高的。当然,我只是举了一个最简单的设计方法,还有很多更加优化的方法,比如将每一个字母从小到大对应一个素数,而不是1,2,3……这样的自然数,这样冲突的概率就会降低一些。
那现在新的问题来了。之前我们只需要比较一下模式串和子串的哈希值,如果两个值相等,那这个子串就一定可以匹配模式串。但是,当存在哈希冲突的时候,有可能存在这样的情况,子串和模式串的哈希值虽然是相同的,但是两者本身并不匹配。
实际上,解决方法很简单。当我们发现一个子串的哈希值跟模式串的哈希值相等的时候,我们只需要再对比一下子串和模式串本身就好了。当然,如果子串的哈希值与模式串的哈希值不相等,那对应的子串和模式串肯定也是不匹配的,就不需要比对子串和模式串本身了。
所以,哈希算法的冲突概率要相对控制得低一些,如果存在大量冲突,就会导致RK算法的时间复杂度退化,效率下降。极端情况下,如果存在大量的冲突,每次都要再对比子串和模式串本身,那时间复杂度就会退化成O(n*m)。但也不要太悲观,一般情况下,冲突不会很多,RK算法的效率还是比BF算法高的。
解答开篇&内容小结
今天我们讲了两种字符串匹配算法,BF算法和RK算法。
BF算法是最简单、粗暴的字符串匹配算法,它的实现思路是,拿模式串与主串中是所有子串匹配,看是否有能匹配的子串。所以,时间复杂度也比较高,是O(n*m),n、m表示主串和模式串的长度。不过,在实际的软件开发中,因为这种算法实现简单,对于处理小规模的字符串匹配很好用。
RK算法是借助哈希算法对BF算法进行改造,即对每个子串分别求哈希值,然后拿子串的哈希值与模式串的哈希值比较,减少了比较的时间。所以,理想情况下,RK算法的时间复杂度是O(n),跟BF算法相比,效率提高了很多。不过这样的效率取决于哈希算法的设计方法,如果存在冲突的情况下,时间复杂度可能会退化。极端情况下,哈希算法大量冲突,时间复杂度就退化为O(n*m)。
课后思考
我们今天讲的都是一维字符串的匹配方法,实际上,这两种算法都可以类比到二维空间。假设有下面这样一个二维字符串矩阵(图中的主串),借助今天讲的处理思路,如何在其中查找另一个二维字符串矩阵(图中的模式串)呢?
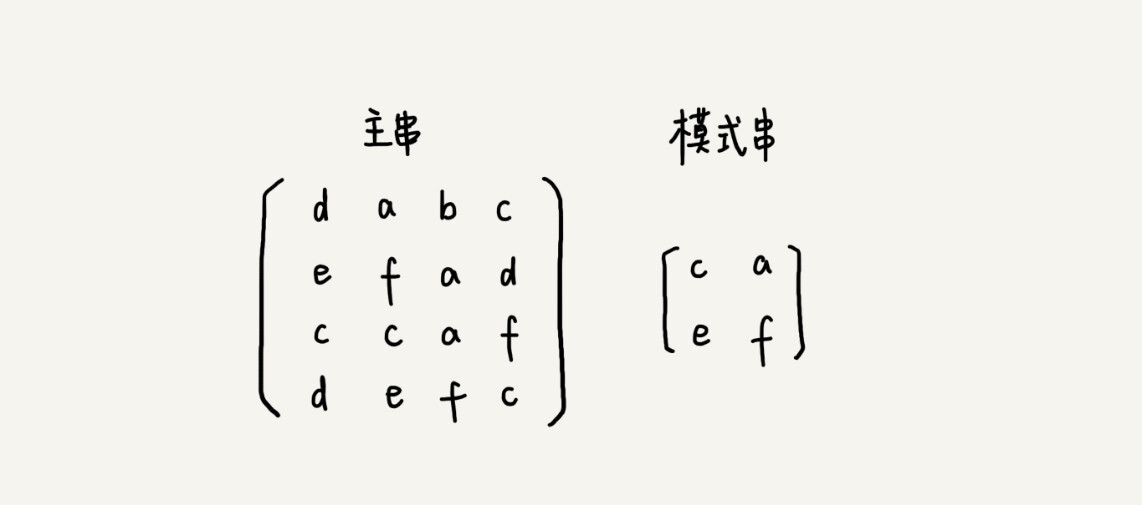
欢迎留言和我分享,也欢迎点击“请朋友读”,把今天的内容分享给你的好友,和他一起讨论、学习。