data-structure-course
20 | 散列表(下):为什么散列表和链表经常会一起使用?
我们已经学习了20节内容,你有没有发现,有两种数据结构,散列表和链表,经常会被放在一起使用。你还记得,前面的章节中都有哪些地方讲到散列表和链表的组合使用吗?我带你一起回忆一下。
在链表那一节,我讲到如何用链表来实现LRU缓存淘汰算法,但是链表实现的LRU缓存淘汰算法的时间复杂度是O(n),当时我也提到了,通过散列表可以将这个时间复杂度降低到O(1)。
在跳表那一节,我提到Redis的有序集合是使用跳表来实现的,跳表可以看作一种改进版的链表。当时我们也提到,Redis有序集合不仅使用了跳表,还用到了散列表。
除此之外,如果你熟悉Java编程语言,你会发现LinkedHashMap这样一个常用的容器,也用到了散列表和链表两种数据结构。
今天,我们就来看看,在这几个问题中,散列表和链表都是如何组合起来使用的,以及为什么散列表和链表会经常放到一块使用。
LRU缓存淘汰算法
在链表那一节中,我提到,借助散列表,我们可以把LRU缓存淘汰算法的时间复杂度降低为O(1)。现在,我们就来看看它是如何做到的。
首先,我们来回顾一下当时我们是如何通过链表实现LRU缓存淘汰算法的。
我们需要维护一个按照访问时间从大到小有序排列的链表结构。因为缓存大小有限,当缓存空间不够,需要淘汰一个数据的时候,我们就直接将链表头部的结点删除。
当要缓存某个数据的时候,先在链表中查找这个数据。如果没有找到,则直接将数据放到链表的尾部;如果找到了,我们就把它移动到链表的尾部。因为查找数据需要遍历链表,所以单纯用链表实现的LRU缓存淘汰算法的时间复杂很高,是O(n)。
实际上,我总结一下,一个缓存(cache)系统主要包含下面这几个操作:
-
往缓存中添加一个数据;
-
从缓存中删除一个数据;
-
在缓存中查找一个数据。
这三个操作都要涉及“查找”操作,如果单纯地采用链表的话,时间复杂度只能是O(n)。如果我们将散列表和链表两种数据结构组合使用,可以将这三个操作的时间复杂度都降低到O(1)。具体的结构就是下面这个样子:
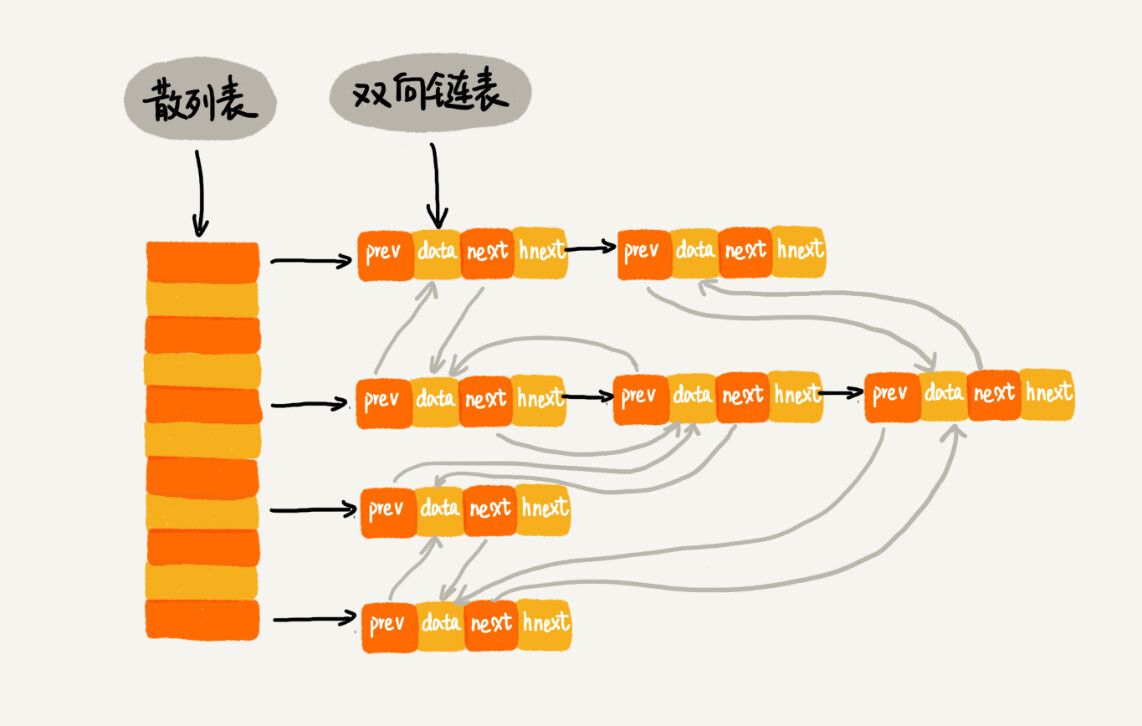
我们使用双向链表存储数据,链表中的每个结点处理存储数据(data)、前驱指针(prev)、后继指针(next)之外,还新增了一个特殊的字段hnext。这个hnext有什么作用呢?
因为我们的散列表是通过链表法解决散列冲突的,所以每个结点会在两条链中。一个链是刚刚我们提到的 双向链表,另一个链是散列表中的 拉链。 前驱和后继指针是为了将结点串在双向链表中,hnext指针是为了将结点串在散列表的拉链中。
了解了这个散列表和双向链表的组合存储结构之后,我们再来看,前面讲到的缓存的三个操作,是如何做到时间复杂度是O(1)的?
首先,我们来看 如何查找一个数据。我们前面讲过,散列表中查找数据的时间复杂度接近O(1),所以通过散列表,我们可以很快地在缓存中找到一个数据。当找到数据之后,我们还需要将它移动到双向链表的尾部。
其次,我们来看 如何删除一个数据。我们需要找到数据所在的结点,然后将结点删除。借助散列表,我们可以在O(1)时间复杂度里找到要删除的结点。因为我们的链表是双向链表,双向链表可以通过前驱指针O(1)时间复杂度获取前驱结点,所以在双向链表中,删除结点只需要O(1)的时间复杂度。
最后,我们来看 如何添加一个数据。添加数据到缓存稍微有点麻烦,我们需要先看这个数据是否已经在缓存中。如果已经在其中,需要将其移动到双向链表的尾部;如果不在其中,还要看缓存有没有满。如果满了,则将双向链表头部的结点删除,然后再将数据放到链表的尾部;如果没有满,就直接将数据放到链表的尾部。
这整个过程涉及的查找操作都可以通过散列表来完成。其他的操作,比如删除头结点、链表尾部插入数据等,都可以在O(1)的时间复杂度内完成。所以,这三个操作的时间复杂度都是O(1)。至此,我们就通过散列表和双向链表的组合使用,实现了一个高效的、支持LRU缓存淘汰算法的缓存系统原型。
Redis有序集合
在跳表那一节,讲到有序集合的操作时,我稍微做了些简化。实际上,在有序集合中,每个成员对象有两个重要的属性, key(键值)和 score(分值)。我们不仅会通过score来查找数据,还会通过key来查找数据。
举个例子,比如用户积分排行榜有这样一个功能:我们可以通过用户的ID来查找积分信息,也可以通过积分区间来查找用户ID或者姓名信息。这里包含ID、姓名和积分的用户信息,就是成员对象,用户ID就是key,积分就是score。
所以,如果我们细化一下Redis有序集合的操作,那就是下面这样:
-
添加一个成员对象;
-
按照键值来删除一个成员对象;
-
按照键值来查找一个成员对象;
-
按照分值区间查找数据,比如查找积分在[100, 356]之间的成员对象;
-
按照分值从小到大排序成员变量;
如果我们仅仅按照分值将成员对象组织成跳表的结构,那按照键值来删除、查询成员对象就会很慢,解决方法与LRU缓存淘汰算法的解决方法类似。我们可以再按照键值构建一个散列表,这样按照key来删除、查找一个成员对象的时间复杂度就变成了O(1)。同时,借助跳表结构,其他操作也非常高效。
实际上,Redis有序集合的操作还有另外一类,也就是查找成员对象的排名(Rank)或者根据排名区间查找成员对象。这个功能单纯用刚刚讲的这种组合结构就无法高效实现了。这块内容我后面的章节再讲。
Java LinkedHashMap
前面我们讲了两个散列表和链表结合的例子,现在我们再来看另外一个,Java中的LinkedHashMap这种容器。
如果你熟悉Java,那你几乎天天会用到这个容器。我们之前讲过,HashMap底层是通过散列表这种数据结构实现的。而LinkedHashMap前面比HashMap多了一个“Linked”,这里的“Linked”是不是说,LinkedHashMap是一个通过链表法解决散列冲突的散列表呢?
实际上,LinkedHashMap并没有这么简单,其中的“Linked”也并不仅仅代表它是通过链表法解决散列冲突的。关于这一点,在我是初学者的时候,也误解了很久。
我们先来看一段代码。你觉得这段代码会以什么样的顺序打印3,1,5,2这几个key呢?原因又是什么呢?
HashMap<Integer, Integer> m = new LinkedHashMap<>();
m.put(3, 11);
m.put(1, 12);
m.put(5, 23);
m.put(2, 22);
for (Map.Entry e : m.entrySet()) {
System.out.println(e.getKey());
}
我先告诉你答案,上面的代码会按照数据插入的顺序依次来打印,也就是说,打印的顺序就是3,1,5,2。你有没有觉得奇怪?散列表中数据是经过散列函数打乱之后无规律存储的,这里是如何实现按照数据的插入顺序来遍历打印的呢?
你可能已经猜到了,LinkedHashMap也是通过散列表和链表组合在一起实现的。实际上,它不仅支持按照插入顺序遍历数据,还支持按照访问顺序来遍历数据。你可以看下面这段代码:
// 10是初始大小,0.75是装载因子,true是表示按照访问时间排序
HashMap<Integer, Integer> m = new LinkedHashMap<>(10, 0.75f, true);
m.put(3, 11);
m.put(1, 12);
m.put(5, 23);
m.put(2, 22);
m.put(3, 26);
m.get(5);
for (Map.Entry e : m.entrySet()) {
System.out.println(e.getKey());
}
这段代码打印的结果是1,2,3,5。我来具体分析一下,为什么这段代码会按照这样顺序来打印。
每次调用put()函数,往LinkedHashMap中添加数据的时候,都会将数据添加到链表的尾部,所以,在前四个操作完成之后,链表中的数据是下面这样:
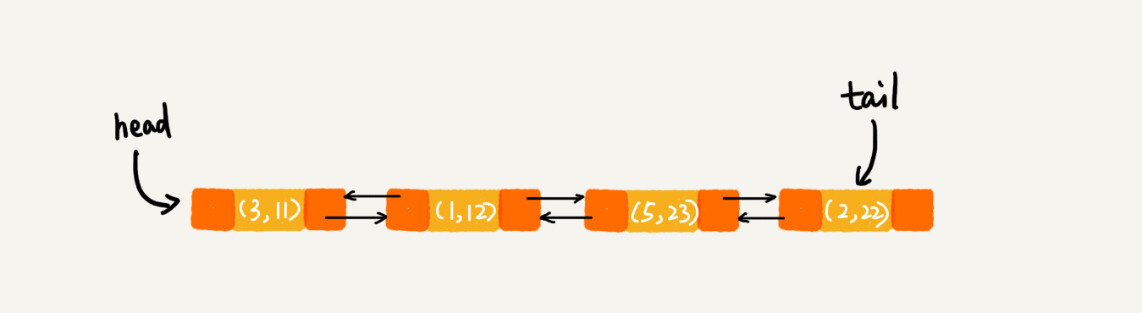
在第8行代码中,再次将键值为3的数据放入到LinkedHashMap的时候,会先查找这个键值是否已经有了,然后,再将已经存在的(3,11)删除,并且将新的(3,26)放到链表的尾部。所以,这个时候链表中的数据就是下面这样:
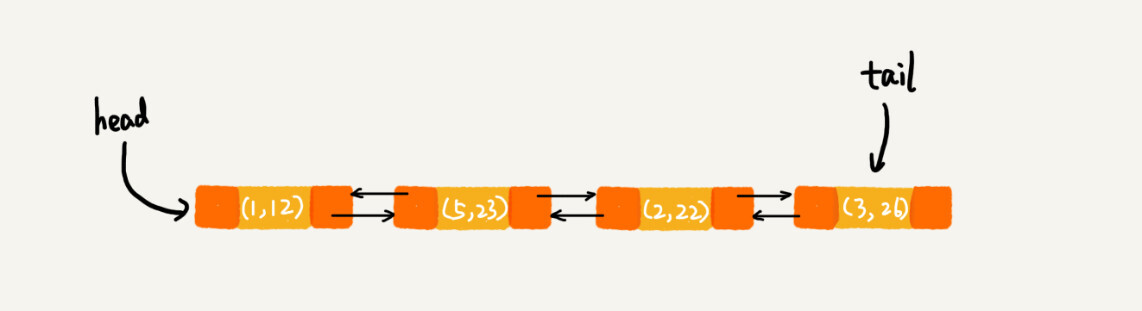
当第9行代码访问到key为5的数据的时候,我们将被访问到的数据移动到链表的尾部。所以,第9行代码之后,链表中的数据是下面这样:
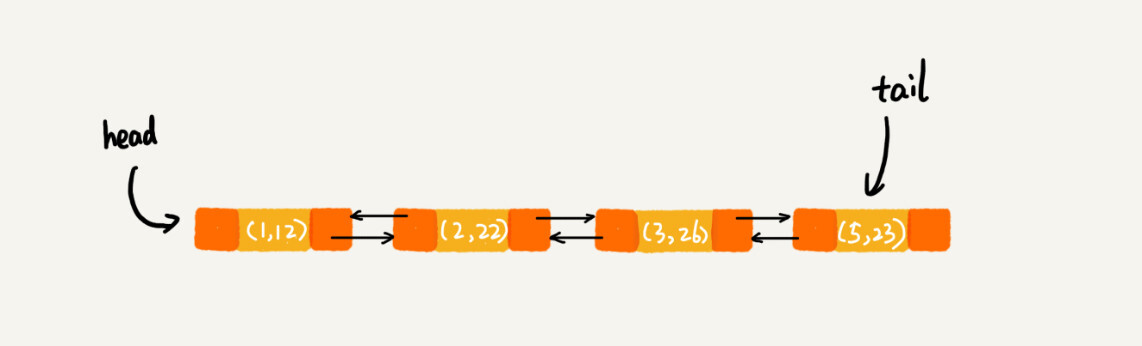
所以,最后打印出来的数据是1,2,3,5。从上面的分析,你有没有发现,按照访问时间排序的LinkedHashMap本身就是一个支持LRU缓存淘汰策略的缓存系统?实际上,它们两个的实现原理也是一模一样的。我也就不再啰嗦了。
我现在来总结一下,实际上, LinkedHashMap是通过双向链表和散列表这两种数据结构组合实现的。LinkedHashMap中的“Linked”实际上是指的是双向链表,并非指用链表法解决散列冲突。
解答开篇&内容小结
弄懂刚刚我讲的这三个例子,开篇的问题也就不言而喻了。我这里总结一下,为什么散列表和链表经常一块使用?
散列表这种数据结构虽然支持非常高效的数据插入、删除、查找操作,但是散列表中的数据都是通过散列函数打乱之后无规律存储的。也就说,它无法支持按照某种顺序快速地遍历数据。如果希望按照顺序遍历散列表中的数据,那我们需要将散列表中的数据拷贝到数组中,然后排序,再遍历。
因为散列表是动态数据结构,不停地有数据的插入、删除,所以每当我们希望按顺序遍历散列表中的数据的时候,都需要先排序,那效率势必会很低。为了解决这个问题,我们将散列表和链表(或者跳表)结合在一起使用。
课后思考
-
今天讲的几个散列表和链表结合使用的例子里,我们用的都是双向链表。如果把双向链表改成单链表,还能否正常工作呢?为什么呢?
-
假设猎聘网有10万名猎头,每个猎头都可以通过做任务(比如发布职位)来积累积分,然后通过积分来下载简历。假设你是猎聘网的一名工程师,如何在内存中存储这10万个猎头ID和积分信息,让它能够支持这样几个操作:
-
根据猎头的ID快速查找、删除、更新这个猎头的积分信息;
-
查找积分在某个区间的猎头ID列表;
-
查找按照积分从小到大排名在第x位到第y位之间的猎头ID列表。
欢迎留言和我分享,我会第一时间给你反馈。