business-algorithm-course

34｜前缀树：Web框架中如何实现路由匹配？

你好，我是微扰君。

不知不觉，已经到工程实战篇的最后一讲了，在这个章节中，我们一起学习了很多工程中常用的算法，如果你从事后端开发，应该或多或少有些接触，比如在Redis、Kafka、ZooKeeper等常用中间件里就经常出现，理解它们的核心思想，能给你的工作带来很大的帮助。

今天，我们最后来聊一聊大部分Web开发工程师都会用到的后端Web框架中的算法。

路由匹配

Web框架的作用，我们都知道，主要就是封装Web服务，整合网络相关的通用逻辑，一般来说也就是帮助HTTP服务建立网络连接、解析HTTP头、错误恢复等等；另外，大部分框架可能也会提供一些拦截器或者middleware，帮助我们处理一些每个请求可能都需要进行的操作，比如鉴权、获取用户信息。

但是所有Web框架，无论设计得多么不同，必不可少的能力就是路由匹配。

因为我们的Web服务通常会对外暴露许多不同的API，而区分这些API的标识，主要就是用户请求 API的URL。所以， 一个好用的Web框架，要能尽可能快地解析请求URL并映射到不同API 的处理逻辑，也就是我们常说的“路由匹配”。

以Golang中常用的Web框架Gin为例，如果用户想注册一套遵循RESTful风格的接口，只需要像这样，写一下注册每个路由所对应的handler方法就完成了：

    userRouter := router.Group("/users")
    {
        userRouter.POST("", user.CreateUser)
        userRouter.DELETE("/:userID", user.DeleteUserByUserID)
        userRouter.GET("/:userID", user.GetUserInfoByUserID)
        userRouter.GET("", user.GetUserList)
        userRouter.PUT("/:userID", user.UpdateUser)
        userRouter.POST("/:userID/enable", user.EnableUser)
    }

例子中userRouter就代表着和用户相关的接口，POST、DELETE、GET等方法标识着HTTP请求的method， 方法里第一个参数就是路由具体的值，也就是URL的值，而第二个参数是一个方法，可以用来实现不同接口的处理逻辑。

这样的路由功能我们是如何实现的呢？

动态路由

每个 HTTP请求都会带上需要访问的URL，Web框架，其实也就是根据这个信息，再通过在用户写出的代码中注册的路由和handler的关系，找到每个请求应该调用的处理逻辑。

所以，如何保存路由和处理方法的对应关系呢？

初看这个问题，估计你一定会有一个非常直接的想法，采用HashMap来存储路由表吧，这样索引起来非常高效。

但是事实上主流的Web框架都不会这样做， 因为利用哈希表存储的路由和处理逻辑的关系，只能用来索引静态路由，也就是路由中没有动态参数的路由，比如 /user/enable time.geekbang.org/hybrid/pvip ，这样的路由，路径是明确的，一个路由只有一种可能性。

但是在Web开发中，我们经常需要在路由中带上参数，这也是RESTful风格的接口所要求的。

最常见的动态参数就是各种ID，比如极客时间的专栏URL，路由中就带了专栏ID的参数 column/intro/100100901 ，这里的 100100901 就是一个特定的参数。虽然参数不同，但所对应的处理逻辑实际上是一致的，在很多Web框架中，这种路由的注册方式一般是写成 /column/article/:id ，其中id的参数就是 100100901 或者其他不同的值，在框架的处理方法里，一般可以通过 context 之类的变量拿到。

这样的路由，就不再是单一的静态路由，而是可以对应某一类型的许多不同的路由，我们也称这种带有参数的路由为“动态路由”。

显然在这种需要支持动态路由的场景下，我们就不太能继续用HashMap记录路由和方法的绑定关系了。那动态路由如何实现呢？方式有很多种，可以用正则表达式匹配来实现，另一种更常用的方式就是我们要重点学习的Trie树。

Trie树

我们先学习一下Trie树这个数据结构。

Trie树，也称为前缀树或者字典树，是一种常用的维护字符串集合的数据结构，能用来做排序、保存、查询字符串，常用场景比如搜索引擎关键词匹配、路由匹配、词频统计和字符串排序等等。

相比于HashMap和Map这样的数据结构，Trie树有一些特别的优势，尤其是上面说的可以适应类似于动态路由匹配的场景，有着不可替代的作用。我们公司的开源产品EMQ X也有用到相关的数据结构来实现MQTT协议路由表。

先简单剧透一下， Trie树主要的特点和优势都建立基于前缀的树状存储方式上。具体是什么样的呢，我们看例子理解。

比如现在想要存储， geek、 geektime、 geekbang、 get、 go 这样几个单词，在trie树上我们是怎么存储的呢？

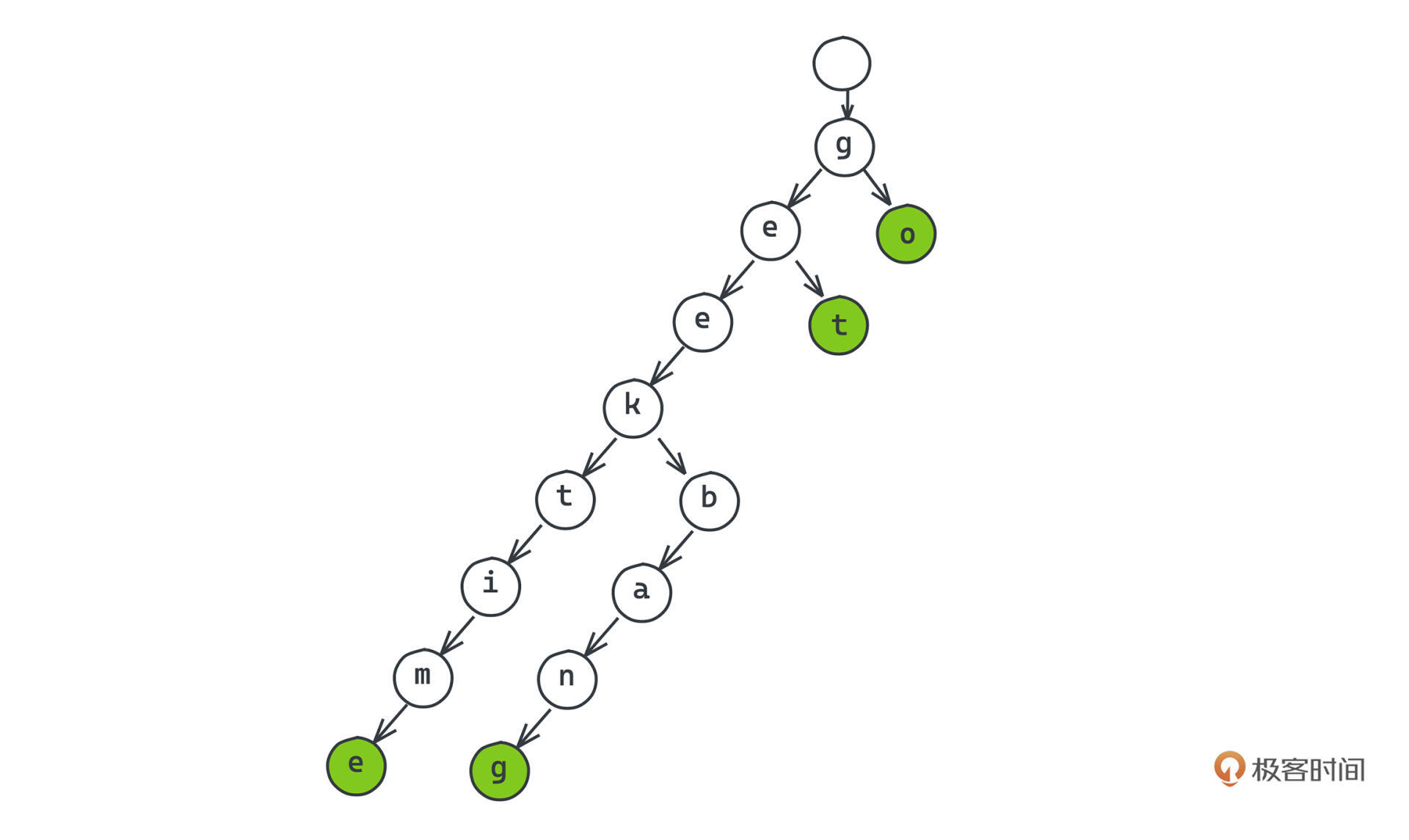
看trie树的示意图。你可以注意到，在trie树中，每个节点都代表着一个字符，且有若干个子节点，对于整个树状图来说，从根节点出发，到任意其他节点构成的路径一定构成我们要存储的字符串集中某一个的前缀，或者就是其本身。

所以，不同于同样是树状结构的二叉查找树实现的treemap，在trie树中，我们存储的字符串并不是直接存储在二叉树的节点中，而是通过节点在树中的位置表示的。我们会为trie树中的结点标记颜色。如果标记为绿色，表示根节点到当前节点的路径是一个集合中的字符串，反之，代表这个节点仅仅是某个字符串的前缀。

显然，相比于treemap来说， trie树存储的开销要小得多，并且因为它天然的前缀匹配和排序的特性，在很多时候也能帮助我们更快检索数据。最常见的比如在搜索引擎的网站中，我们有时候输入一部分内容，搜索框可能就会自动补全一些可能的选项，很多时候这个小功能的实现，用的就是前缀树前缀匹配的特性。

前缀树具体如何用代码来实现呢？

前缀树实现

首先，我们还是要先用代码定义一下前缀树的结构体。

为了方便讲解，我们就假设前缀树只存储英文单词，所以我们的字符集只包括26个小写字母。那在这样的情况下，用来表示每个节点的子节点也不用开动态数组了，直接开一个26维的静态数组就可以，下标0～25正好可以对应a～z这26个字母。

同时，每个节点还需要像前面说的那样标记一下自身的颜色，我们用isKey来表示当前节点是集合中的单词还是只是某些单词的前缀。

写成C++代码如下：

    struct trie_node
    {
        bool isKey;   // 标记该节点是否代表一个关键字
        trie_node *children[26]; // 各个子节点
    };

现在有了基本的数据结构定义，我们自然也需要进行初始化、插入、查询等操作。先来看初始化和插入的过程。

一开始，我们只有一个代表空串的空节点，所以初始化的过程很简单，就是创造一个空的根节点，其子节点也都是空指针；同时因为空节点不代表任何串，isKey必然也是false。

class Trie {
    trie_node* root;
public:
    Trie() {
        root = new trie_node();
        root->isKey = false;
        for (int i = 0; i < 26; i++) {
            root->children[i] = NULL;
        }
    }

    /** Inserts a word into the trie. */
    void insert(string word) {
        trie_node* node = root;
        // 循环判断单词的每个字母是否被当前节点node的子节点所包含
        for (auto ch: word) {
            // 不包含则需要创建
            if (node->children[ch-'a'] == NULL) {
                node->children[ch-'a'] = new trie_node();
                node->children[ch-'a']->isKey = false;
            }
            // 否则将当前节点指向下一个节点继续这个过程
            node = node->children[ch-'a'];
        }
        // 遍历完成时，当前节点的位置就是一个被包含于字符集的串；需要将标记置true
        node->isKey = true;
    }
}

具体的插入过程，其实就是要沿着根节点，根据插入单词每一位的字母，一路往下遍历，选择合适的分支，判断每个字母是否被trie树所包含，如果遇到尚未被包含的字母，我们需要在对应字母的位置创建节点，并循环这个过程，直到整个单词的每个字母都被添加到trie树中。

最后，记得把单词的最后一个字母节点的isKey标记置为true，表示这个单词被成功加入集合。

有了插入过程的基础，搜索的过程理解起来就很简单了，沿着trie树一路搜索单词的每个字母，直到遇到空的子节点， 或者最后遍历完成发现当前节点的isKey为false，这代表所有字母虽然都在trie树中存在，但这只是某个单词的前缀，而不是全部；如果最后一个字母在trie树中且isKey为true，说明单词存在于集合中，我们找到了它。

    /** Returns if the word is in the trie. */
    bool search(string word) {
        trie_node* node = root;
        for (auto ch: word) {
            // 字母不存在
            if (node->children[ch-'a'] == NULL) return false;
            node = node->children[ch-'a'];
        }
        // 仅仅是前缀
        return node->isKey;
    }

我们来简单分析一下前缀树的复杂度。

假设查询的单词平均长度为n，字符集大小为t。对于查询和插入来说，我们所做的就是遍历一遍整个单词并在树上创建节点或者移动，时间复杂度和插入单词的平均长度一致，为O(n)。

空间复杂度相对差一些，上面的实现方式里，由于我们为每个节点都开了字符集大小的数组，所以空间复杂度是O(t*N)，其中N是节点的数量，最差是所有单词的长度和。

Trie树在路由匹配中的应用

好了，相信你现在已经理解了trie树是如何工作的了，那它是如何用于动态路由匹配的呢？

首先对于静态路由，相信你应该已经猜到了，我们只需要稍作调整，从每个节点表示一个字符，变成每个节点表示路由被 / 分割的一节，比如图片里，我们就存储了两条静态路由 /users 、 /users/register ：

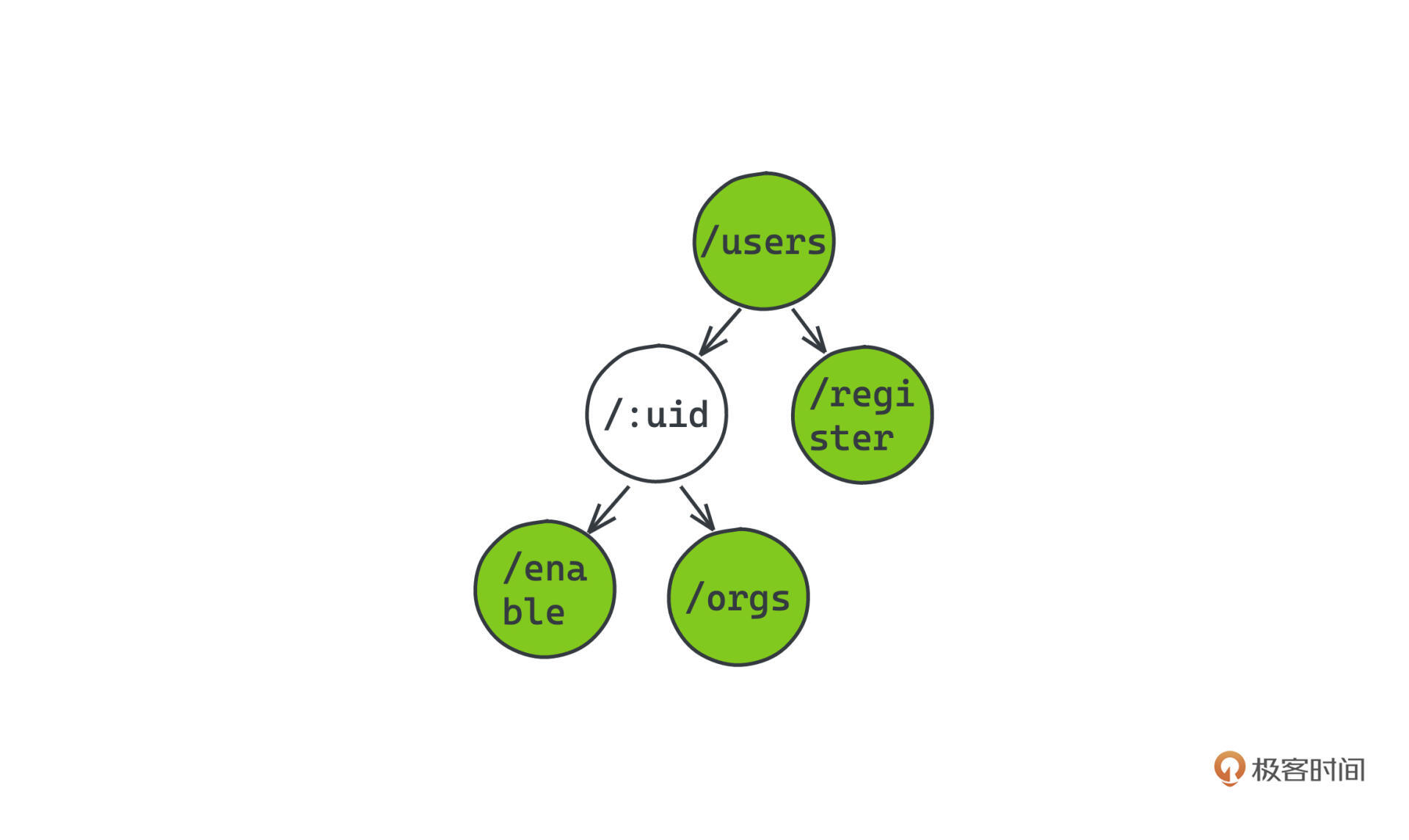
而动态路由，表示起来其实是一样的，只不过，我们在匹配下一层节点的时候会优先匹配有静态路由规则的值，如果没有匹配上，同一层又有其他动态路由的占位符号，我们才会去认为对应的URL匹配的是动态路由中的动态参数。

比如 /users/register 肯定会匹配 /users/register，但是 /users/regissss/enable 会匹配到 /users/:uid/enable，并把 regisss 当成 /:uid 传入对应URL的handler中。

除此之外，插入和查询的过程，和前面讲的的trie树实现是一致的，感兴趣的话你可以自己动手写一个Web框架感受一下，或者去查阅一些经典路由框架的源码，一定会有很多收获的。

总结

前缀树，采用了独特的树状存储结构，是一种高效的有序集合的实现，通常集合元素存储的是字符串。但是不同于treemap直接在节点中存储键，前缀树在节点中存储的是某个串的一个组成单元，对于字符串来说通常就是一个字符；集合中的每个元素由节点在树中的位置来标记，根结点到每个标记为key的节点的路径，构成了集合中的所有元素。

也正是因为这样的特性，前缀树天然就做到了对集合的字典序的维护，特别适合各种前缀匹配的场景，在字符串检索、敏感词过滤、搜索推荐、词频统计等场景中多有应用。我们Web框架动态路由的功能也多是基于trie树实现的。另外力扣上就有一道实现前缀树的题目，你可以试着做一做。

课后思考

今天留给你两个课后思考题。

可以尝试自己实现一下trie树和基于trie树的路由匹配逻辑，看看在路由匹配的场景下，我们是否需要做一些什么不同的改造。
文中给出了一种trie树的C++实现，其中提到这种实现的空间效率不是很好，主要原因就在于我们为每个节点都开了等同于字符集大小的数组，但其中显然很大一部分都存的是空指针。你有没有什么办法优化呢，优化后会出现什么新的问题吗？

欢迎你在评论区留下你的思考，如果觉得这篇文章对你有帮助的话，也欢迎转发给你的朋友一起学习～