business-algorithm-course
17|选路算法:Dijkstra是如何解决最短路问题的?
你好,我是微扰君。
在掌握操作系统中的一些经典算法之后,我们来学习计算机的另一大基础课——计算机网络中的算法。计算机网络,当然也是一个历史悠久的科研方向,可以说之所以现在计算机世界如此繁荣,计算机网络发挥着巨大的作用,是整个互联网世界的基石。
复杂的计算机网络中自然也产生了许多算法问题,比如许多经典的图论算法都是在计算机网络的研究背景中诞生的。在这一章我们会挑选几个有趣的问题一起讨论,主要涉及两种场景,计算机网络网络层的选路算法、传输层协议TCP中的滑动窗口思想。
今天我们先来学习选路算法,有时它也被称为路由算法,“路由”这个词相信你应该很熟悉,没错,说的就是路由器里的路由。
路由
我们知道,计算机网络的作用,就是通过把不同的节点连接在一起从而交换信息、共享资源,而各个节点之间也就通过网络形成了一张拓扑关系网。
比如在一个局域网下,节点A要给节点B发送一条消息,如果A和B并没有直接通过网络相连,可能就需要经过其他路由设备的几次转发,这时我们需要在整个网络拓扑图中找到一条可到达的路径,才能把消息发送到目的地。
每台路由器都是一台网络设备,也就是网络中的一个节点,在其中就保存有一张路由表, 每次网卡收到包含目标地址的数据包(packet)时,就会根据路由表的内容决定如何转发数据。
你的电脑也是一个网络上的一个节点,我们在Mac上通过命令就可以看到自己节点的路由表:
netstat -nr
我本地获取到的路由表如下:
Routing tables
Internet:
Destination Gateway Flags Netif Expire
default 192.168.1.1 UGSc en0
127 127.0.0.1 UCS lo0
127.0.0.1 127.0.0.1 UH lo0
169.254 link#6 UCS en0 !
192.168.1 link#6 UCS en0 !
192.168.1.1/32 link#6 UCS en0 !
192.168.1.1 f4:1c:95:6d:c0:e8 UHLWIir en0 1125
192.168.1.7/32 link#6 UCS en0 !
192.168.1.7 3c:22:fb:94:7:cf UHLWI lo0
192.168.1.8 22:6:ba:99:db:c5 UHLWIi en0 847
192.168.1.11 f6:f0:14:1b:9f:68 UHLWIi en0 1002
192.168.1.12 ae:ea:e4:f2:a4:69 UHLWI en0 1063
224.0.0/4 link#6 UmCS en0 !
224.0.0.251 1:0:5e:0:0:fb UHmLWI en0
239.255.255.250 1:0:5e:7f:ff:fa UHmLWI en0
255.255.255.255/32 link#6 UCS en0 !
路由表的每一行都代表一条路由规则,至少会包括两个信息,也就是路由表的前2列:
- 目标网络地址(Destination):标示IP包要去往的目标网络
- 下一跳地址(Gateway):与当前路由器相邻的路由器,命中这条规则的数据包应该经由这个路由器转发去往最终目的地
这里的后3列我也顺带简单介绍一下,flag是路由的一些信息,netif指的是网络物理接口,expire代表过期时间,你感兴趣的话可以去查阅Linux手册详细了解。
因为每个数据包里包含了目标地址,所以路由器工作的基本原理就是,网卡基于路由表匹配数据包对应的规则,转发到下一跳的路由器直至抵达终点就可以了。
路由表
那这个路由表怎么来呢?主要有两种方式。
一种就是我们手动管理配置。Linux提供了简单的配置命令,既可以根据路由IP配置路由表,也可以基于一定的策略配置,查阅Linux手册即可。这种方式也被称为静态路由表,最早期的网络就是这样由网络管理员手动配置的。但如果网络结构发生变化,手工修改的成本就非常高。
为了解决这种问题,第二种方式——动态路由表就应运而生,它可以根据协议在网络中通过节点间的通信自主地生成,网络结构变化时,也会自动调整。
而生成动态路由表的算法,就是我们的选路算法。所以, 选路算法所做的事情就是,构建一个动态路由表,帮每个数据包都选择一条去目标IP最快的路径。
那在路由选路问题中,什么是最快路径呢?
我们知道信息在网络上传输肯定是需要经过物理传输的,各设备之间的距离以及不同设备本身的网络连接情况都是不同的,都会影响节点间传输的时间。如果我们把不同节点之间的通信时间当作距离, 整个拓扑图上搜索最快路径的过程,其实就等价于求图上的最短路问题。
求解最短路的算法,相信你也学过不少了,比如基于BFS的SPFA、基于贪心思想的Dijkstra、基于动态规划思想的Bellman-Ford等算法。这些算法在选路问题中也有应用,最经典的两种就是基于Dijkstra实现的链路状态算法和基于Bellman-Ford实现的距离矢量算法。
今天我们就来先学习鼎鼎大名的Dijkstra算法,看看它是如何解决最短路问题的(链路状态算法和距离矢量算法在后两讲学习)。
Dijkstra算法
Dijkstra算法是一个非常经典的求解单源最短路(Single Source Shortest Path)问题的算法,但它有一个巨大的限制:只能用于没有权重为负的边的图。
在分析这一限制之前,我们还是先来严谨地定义一下最短路问题。
假设我们有一张图G=(V,E),图中共有v个节点,它们之间有e条无向边。其中,各节点的集合用V表示,边的集合用E表示,边权weight就代表该边两点之间的距离。
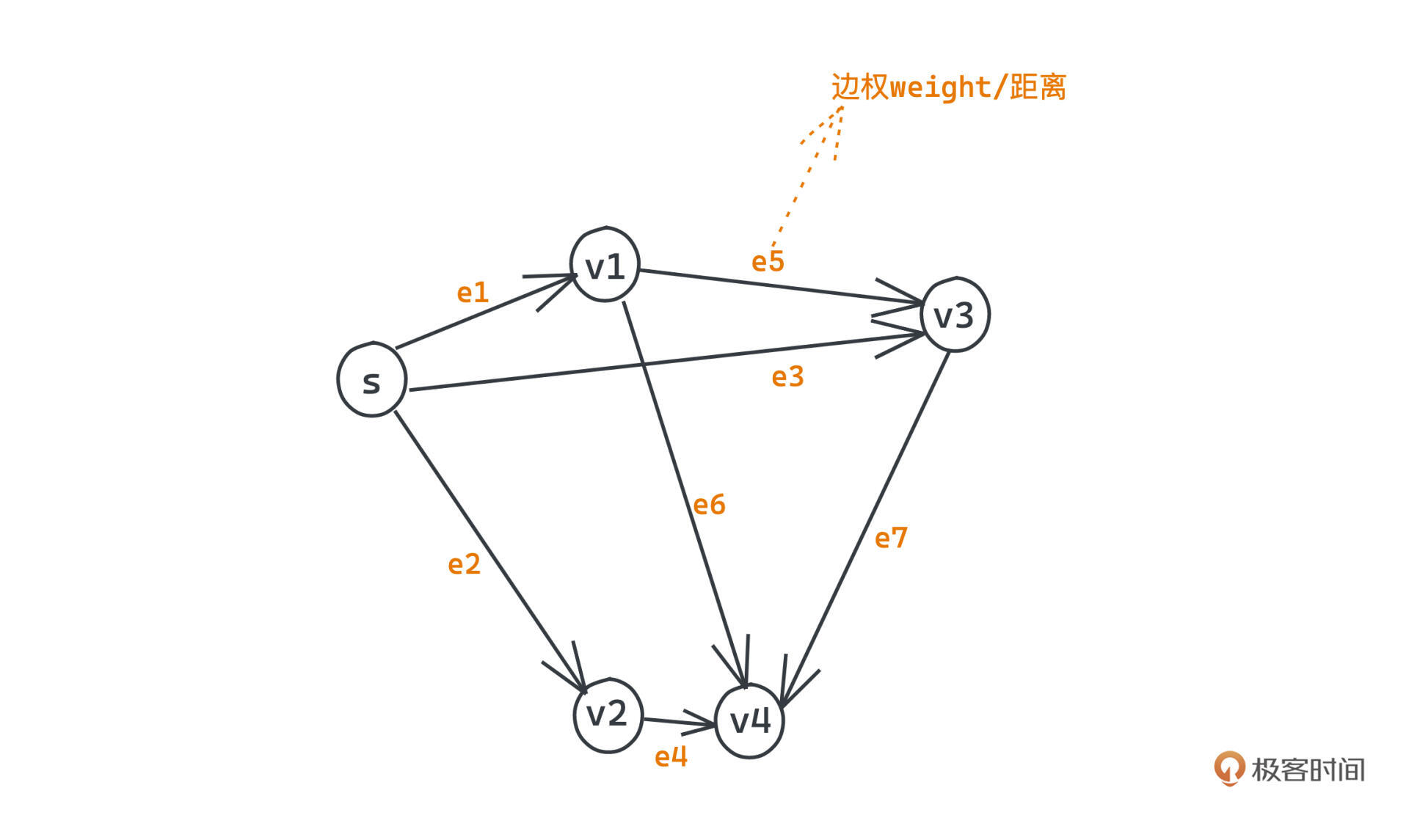
单源最短路问题就是要在这张图上求出从源点s到图上任意其他点的距离最短的路径,一条路径的长度/距离大小就是这条路径上所有边的权重和。具体怎么做呢?
估计你也想到了,一个比较直觉的思路就是贪心思想,我们从离s最近的点开始记录,然后找次之的点、再次之点,逐步推进。
- 我们先找出距离源点s最近的节点
它一定是和s直接相连的节点中距离最近的一个,这是因为所有和s构成二度关系的节点都会经过一个和s直接相连的节点,距离不会短于这个直接相连的节点,所以这个节点一定是所有节点中到s距离最近的节点,我们把这第一个节点记录为v1。
- 然后再找出距离s次近的节点
这时刚找到的v1就有可能成为次短路径的一部分了,我们需要在和s、v1直接相邻的节点中,再次找出除了v1之外到s距离最短的节点,它一定是剩余节点中到s最近的节点。
- 依次类推,就可以求出s到所有节点的最短路径了
Dijkstra算法其实就是这样做的,它引入了一种叫做最短路径树的构造方法。按照刚才说的基于贪心的思想逐步找出距源点s最近、次近的点,就能得到一个G的子图,里面包含了s及所有从s出发能到达的节点,它们以s为根一起构成了一颗树,就是最短路径树。找到了这颗树,我们自然也就求出了s到所有节点的最短距离和路径了。
思路
为了把我们刚才直觉的想法用编程语言更精确的描述出来,需要引入一种叫做“松弛(relax)”的操作,结合例子来讲解这个过程。
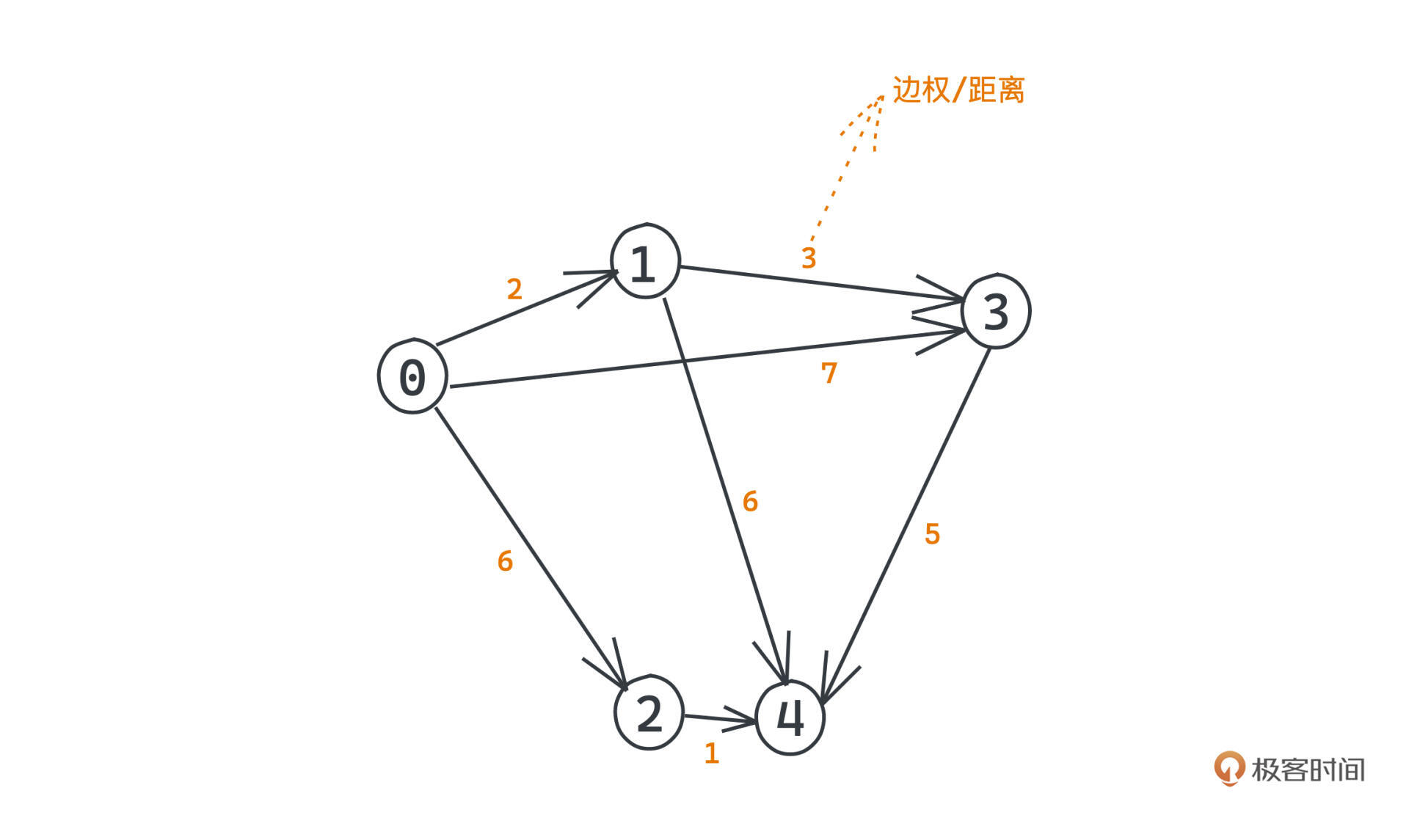
假设现在有了一张有向图G,其中包含了0、1、2、3、4这5个节点,节点之间的边权代表距离,都标在图上了,比如节点0和节点1之间的边权/距离是2。
假设0节点是源点s,我们如何构造出这棵以s为根的最短距离树T呢?
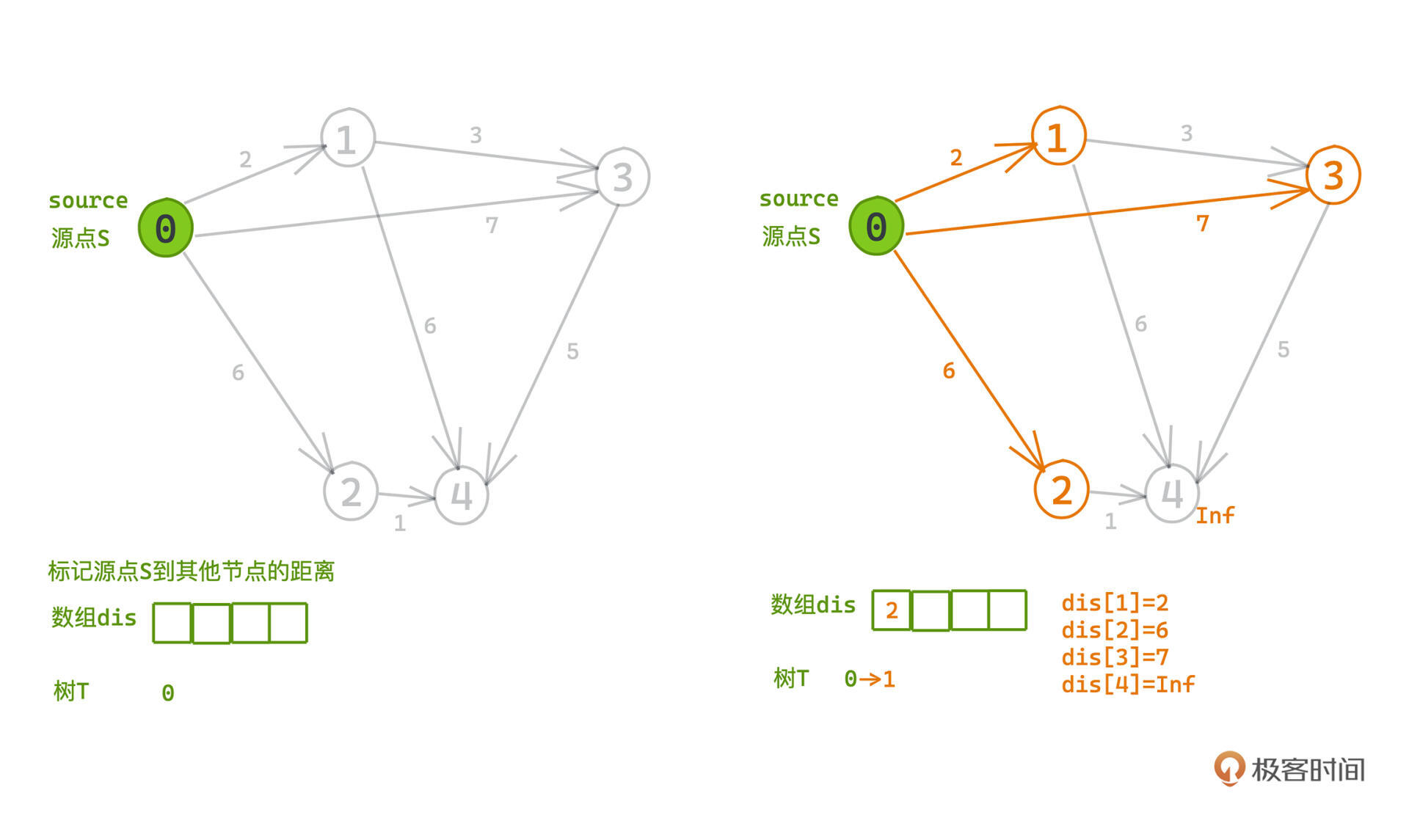
整个构造过程是一步步从原点向外扩张的,我们可以用一个 数组dis 标记源点s到其他节点的距离。由于刚开始树T中只有根节点s,此时:
- 大部分不和s直接相邻的节点到s的距离都是未知的,我们可以暂时记录为 Inf,代表无限大;
- 和T直接相邻的节点就是我们的候选节点,在最开始时也就是s的所有邻节点。我们每次从中选择距离s最短的一个节点加入树T中,只需要遍历所有节点到s的距离就可以得到这个节点,我们记作 u。
比如对于节点0而言,1就是目前候选集里到s最近的节点。
那每次挑出最短节点u加入T中之后,T的候选集显然就多了一些选择,u的所有相邻的节点以及它们到树的距离都可以被发现了。
但u的邻节点v,到源点s的距离有两种可能。
-
第一种情况dis[v] = Inf,代表这个节点v 还没有被加入过候选集中,也就是之前和源点s不直接相邻。
比如图中从1节点搜索4节点的时候就是这种情况。我们可以把v加入T中,并记录dis[v] = dis[u]+edge[u][v],这很显然是 目前发现的、能到v的最短距离,但它依旧有可能在后续遍历过程时被更新,我们叫做“松弛操作”。
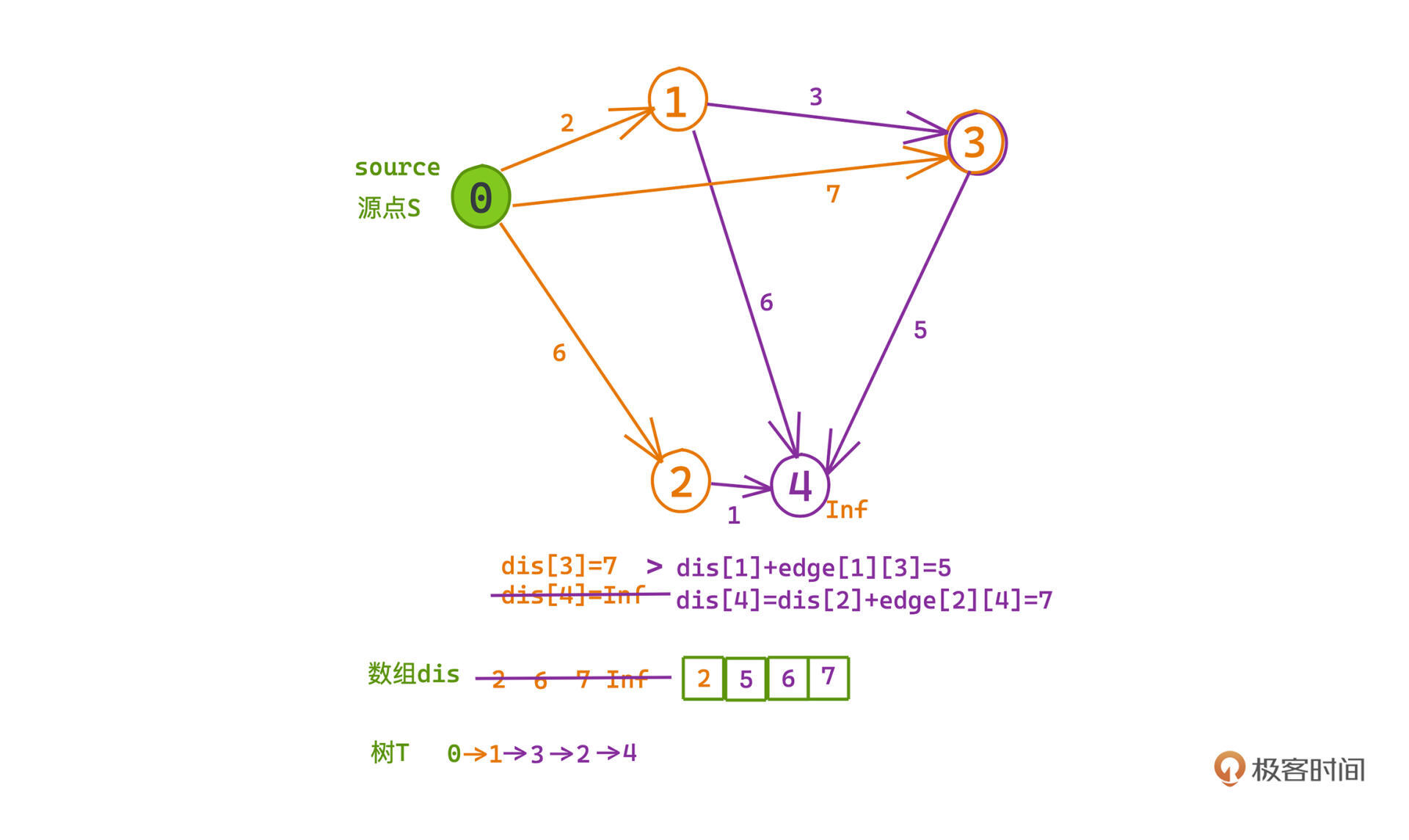
-
第二种情况dis[v]!=inf,这说明v已经被加入到候选集中了,也意味着之前有其他路径可以到达v。
这个时候,我们要比较一下经由u到达v是不是一条更短的路径,判断 dis[u]+edge[u][v] 是否小于 dis[v],如果小于就要更新 dis[v] = dis[u] + edge[u][v]。比如图中从1节点搜索3节点的时候就是这种情况。
更新的操作其实就是“松弛”,不过我个人觉得“松弛”不是一个很好理解的说法,因为松弛操作实际上 是让这条路径变得更短,不过因为Dijkstra是用“relax”来描述这个更新操作的;所以我们也翻译成松弛操作。
我们再来一起结合例子梳理一遍搜索的全过程。
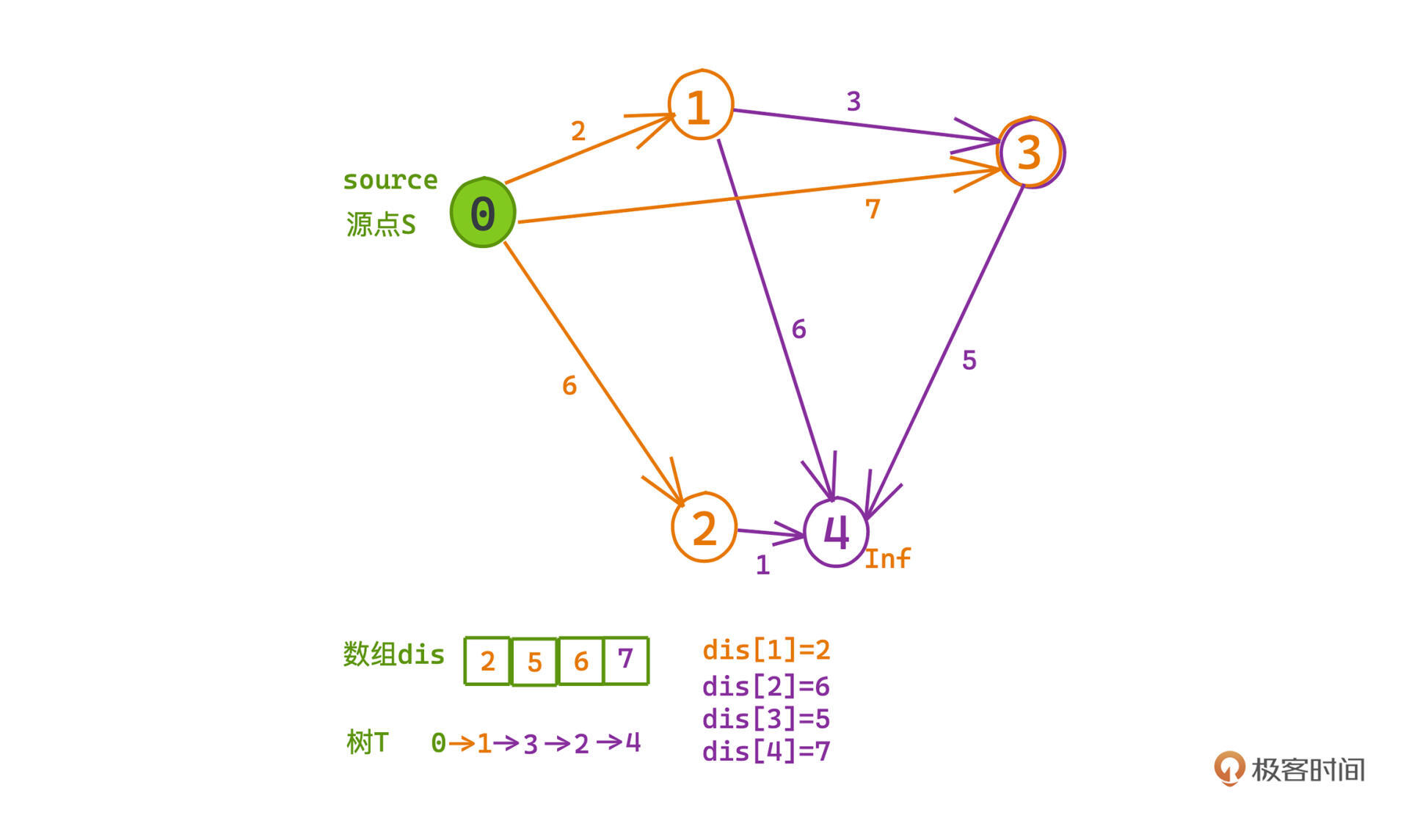
在整个构造过程中会依次把0、1、3、2、4节点入队,入队时,它们都是候选集到s中距离最短的节点。
在没有负边的情况下,这就保证了剩余的节点距离一定长于这个节点,也就不会出现入队之后节点距离仍然需要更新的情况,每个加入树中节点的距离在加入的那一刻就已经被固定了。
入队的时候,我们也探索到了一些 可能和树相接且到s更近的节点,需要对它们进行“松弛”,并加入候选集合。
比如0-3节点的距离开始是7:但在1节点加入候选集之后,我们就可以经由1去往3,这时3到0的距离就会被更新为5,而不再是7了;这个时候3节点(0-1-3)已经是所有剩余节点中到s最近的节点了,我们把它加入树中,dis[3]=5也不会有机会再被其他节点更新了。
代码
理解了这个过程,翻译成代码也就比较简单了,力扣上的 743网络延迟时间 就是一道典型的最短路应用题,有多种解法。
这个题正好是建立在网络的场景下的,求从源点s出发把消息广播到所有节点的时间,节点之间的边就代表着网络传输的延时,也就是求s到图上所有节点最短距离的最大值。
用我们今天学的Dijkstra算法就可以求解,实现代码贴在这里供你参考:
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
// 标记未被探索的节点距离
const int inf = INT_MAX / 2;
// 邻接表
vector<vector<int>> g(n, vector<int>(n, inf));
// 构图
for (auto time: times) {
g[time[0] - 1][time[1] - 1] = time[2];
}
vector<int> dist(n, inf); // 所有节点未被探索时距离都初始化为无穷
vector<bool> used(n, false); // 标记是否已经被加入树中
dist[k - 1] = 0; // 记录原点距离为0
for (int i = 0; i < n; ++i) {
int x = -1;
// 找出候选集中到S距离最短的节点
for (int y = 0; y < n; ++y) {
if (!used[y] && (x == -1 || dist[y] < dist[x])) {
x = y;
}
}
// 加入树中
used[x] = true;
// 基于x 对所有x的邻节点进行松弛操作
for (int y = 0; y < n; ++y) {
dist[y] = min(dist[y], dist[x] + g[x][y]);
}
}
// 取出最短路中的最大值
int ans = *max_element(dist.begin(), dist.end());
return ans == inf ? -1 : ans;
}
};
代码中的dist用于标记距离,used用于标记树中的节点,每次我们都会从候选节点中挑选出到s最短的节点,并基于它对其邻节点进行“松弛”操作;等整个最短路问题求解完毕,最后再从所有距离中取出最大值就可以了。
时间复杂度也很好分析,整个代码中一共有两层循环,外层循环就是每次把一个节点加入树中,一共进行n次;内层循环有两段,分别用于找出最短节点和对所有邻居进行“松弛”操作,最多也不会超过2*n次计算。所以,整体时间复杂度为O(n^2)。
总结
网络路由算法,核心就是在动态变化的网络中,基于探测和寻找最快传输路径的想法,帮助路由器建立路由表,让每个数据包都可以快速且正确地传播到正确目的地。
首先我们需要想办法解决最短路的问题,Dijkstra就是这样一种在没有负边的图中求解单源最短路的算法,基于贪心的思想,我们构造一颗最短路径树就可以求出从源点到网络中所有节点的最短路径了。核心的就是松弛操作,每次加入一个最短节点之后,我们还需要基于它去探索一遍和它相临的节点是否距离更短,比如从不可达变成可达,或者从一条更长的路变成一条更短的路。
Dijkstra算法实现起来还是有一定难度的,你可以多去力扣上找几道题目练手检验一下学习效果;另一个有效的检验方式就是参考费曼学习法,你可以试着给你的朋友讲一下为什么Dijkstra算法不支持负边,这也是Dijkstra算法非常重要的一个约束,如果能讲清楚你也就理解精髓了。
有了Dijkstra算法,我们也就可以求解网络路由中的最短路问题了。后两讲学习我们将学习最经典两种路由的算法:基于Dijkstra算法实现的链路状态算法、基于Bellman-Ford实现的距离矢量算法。
课后作业
最后也给你留一个简单的课后思考题。我们分析了Dijkstra算法的时间复杂度为O(N^2),你觉得是不是可以有更快的写法呢?
欢迎你在留言区与我讨论,如果你觉得本文有帮助,也欢迎你分享给你的朋友一起学习。我们下节课见~
参考资料
每个数据包里包含了目标地址,具体还有哪些内容,你可以去补习一下计算机网络的基础内容,推荐学习UW的 计算机网络 课。