business-algorithm-course
07|堆:如何实现一个高效的优先队列?
你好,我是微扰君。
上一讲学习了基于红黑树的ordered_map的实现,今天我们来介绍另外一种有趣的树,heap,也就是堆。堆的应用非常广泛,我们常说的堆排序的堆就是指这种树状数据结构,除此之外还可以用来解决诸如TopK,或者合并多个有序小文件之类的问题。
堆也是我们最后一个基础数据结构容器-优先队列的常见底层实现方式。
优先队列
你一定还记得之前讲过的线性数据结构queue吧,也就是队列,一种先进先出的数据结构,生活中这种先进先出的场景也很常见,我们当时举了一个在餐厅排队取号的例子,先来的人一定会先取到号,也先被叫到号,这完美地符合队列的语义。
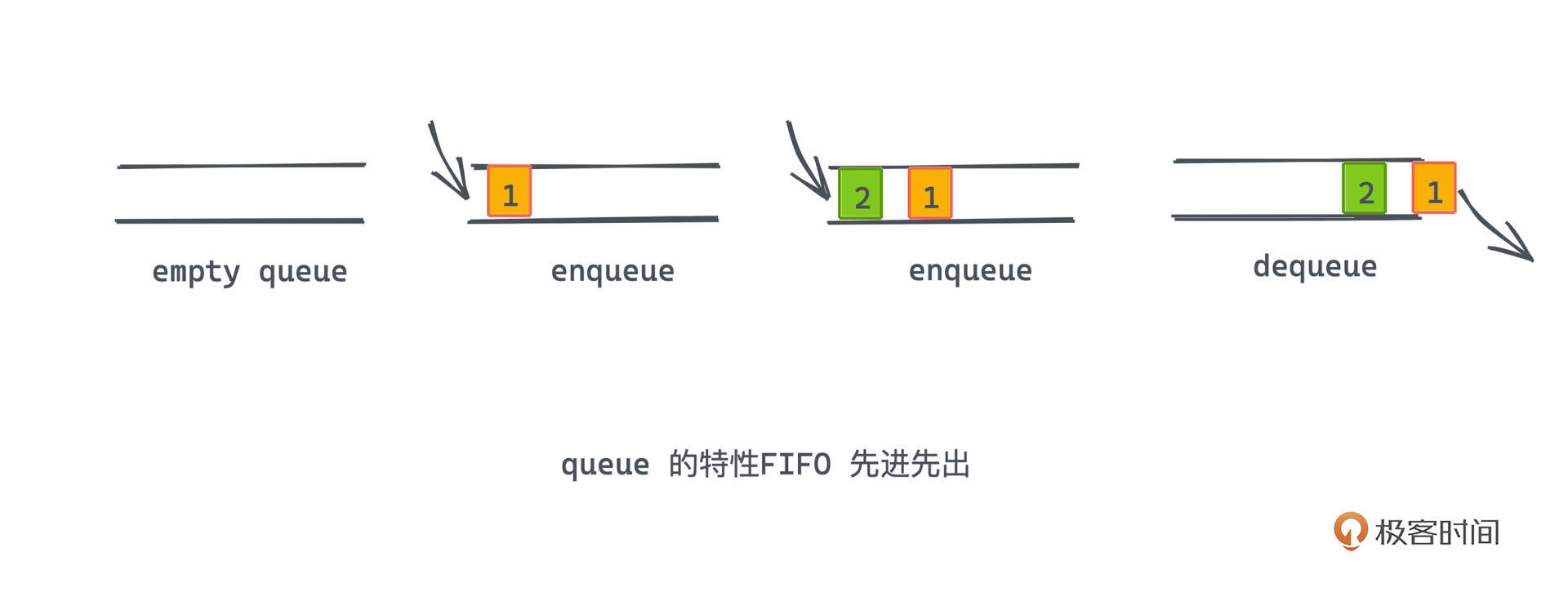
那如果我们现在希望允许一部分人插队呢?比如在医院中,大部分病人都有序的挂号排队,但这时候如果来了一个重症病患,我们就很可能需要破坏先进先出的规则,让医生优先诊断治疗这位病患。这种场景中的队列,我们就可以定义为“优先队列”。
优先队列中的每个元素,我们会赋予它一个优先级,优先级相同的元素我们还是遵循先进先出的原则, 但一定会保证队列中优先级更高的元素先出队,即使它进队时间更晚。比如例子中的重症病患来的并不早,但依旧得到了医生的优先治疗。
对于这种优先队列,我们应该如何高效地实现呢?
如何实现
其实也很容易想到不止一种方案。
比如,一种比较暴力的思路可以是:我们依旧用线性容器存储元素。在入队的时候,我们不关心优先级的影响直接按顺序存入容器中, 出队的时候,则遍历容器找到最高优先级的元素出队。
由于入队的时候没有对优先级做任何处理,所以出队的元素显然可能在线性容器中任意一个位置,基于之前所学的知识,遇到节点删除的场景,用链表显然比用动态数组有更好的时间复杂度。但即使如此,每次出队时我们也需要遍历链表,所以时间复杂度为O(N)。
那与之相对的,另一种同样基于链表的思路也可以是, 我们每次在入队的时候进行一些额外的调整,使得整个队列一直满足优先级更高的元素在更前面的约束,这样出队的时候就比较简单。当然这样会导致入队的时候都需要进行一次类似于插入排序的操作,最差情况下也会要遍历完整个链表,时间复杂度同样为O(N)。
假设出队和入队操作数量相等,均摊下来,每一次操作的时间复杂度就是O(N)。
看示意图辅助你理解,队列里的数字代表权重,a、b、c、d、e 代表着入队的值,我们假设入队顺序和值的字典序是一致的。上面的队列画的就是入队的时候就按照优先级排好序的情况,所以直接从队尾出队即可;下面的队列是入队的时候直接放到队尾,出队的时候要按照优先级取出元素。
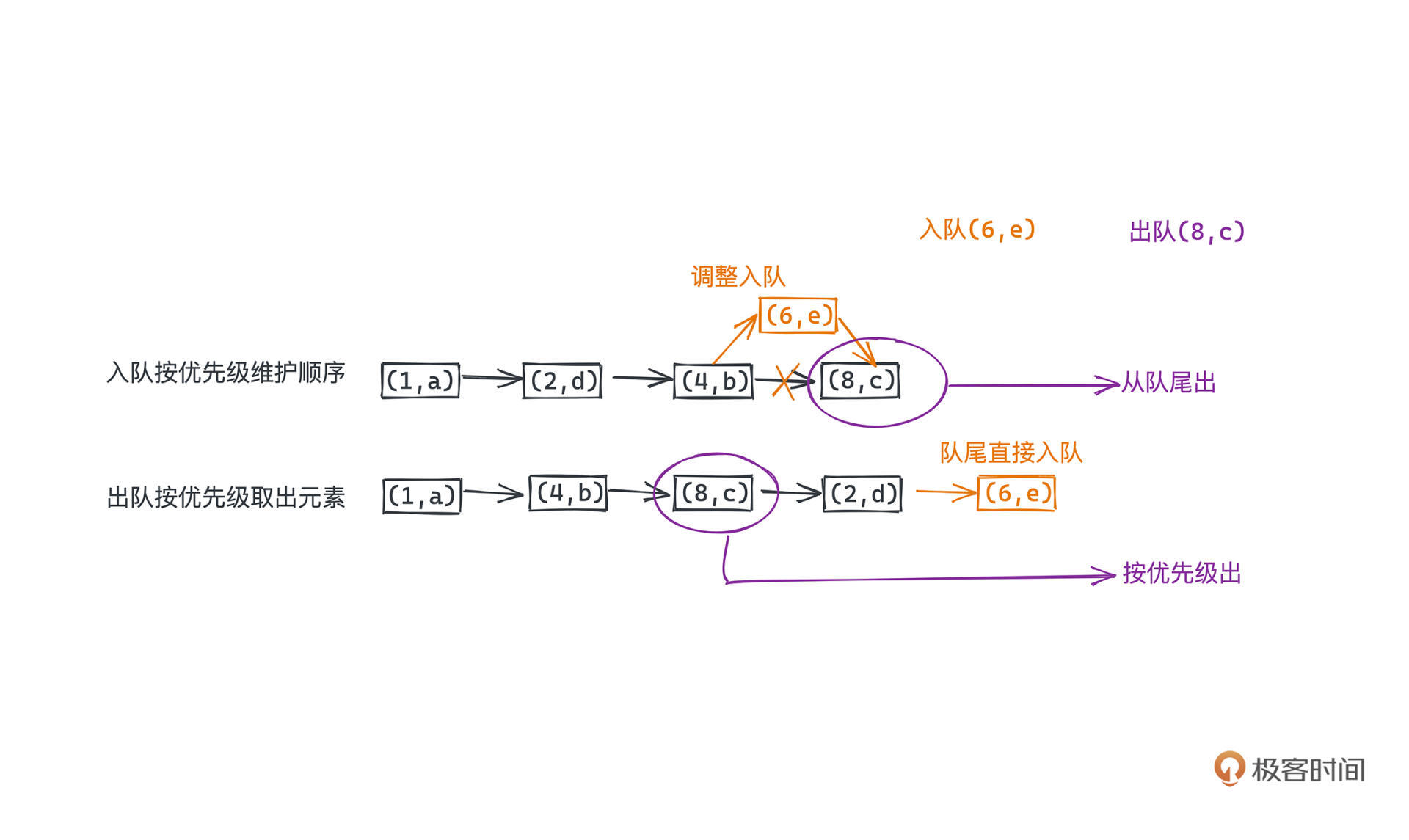
那有没有一种入队和出队都相对来说比较高效的方式呢?答案是肯定的, 只是我们需要抛弃线性的存储结构。
不知道你是不是也想到了上一章讲的红黑树。其实你的想法是对的,红黑树当然是可以用来实现优先级队列的一种方式,我们建红黑树的时候以优先级为key作为排序依据即可。入队的时候可以直接push入队,出队pop的时候先从树中找到优先级高的,也就是树的最右节点,然后移除即可。
这些操作的复杂度都是O(logN),所以出队和入队的复杂度自然也就是O(logN)。所以,基于红黑树的优先队列复杂度均摊下来,相比于之前基于线性表的O(N)复杂度,显然更胜一筹。
但是由于我们不会进行类似“找出优先级第3高的元素出队”这样的操作, 其实并不需要一直维护完全的顺序信息,只是需要能在每次出队时,找到优先级最高的元素即可。那有没有更合适的选择呢?
相比复杂的红黑树,简明的“二叉堆”就是这样一种特别适合用来动态维护一组元素中最大或者最小值的数据结构,它也是各大语言实现优先级队列的首选。
二叉堆
二叉堆,这个数据结构是1964年斯坦福大学教授Robert W.Floyd和J.Williams在发明堆排序的时候提出,之所以想介绍一下它的历史,主要是因为Robert W.Floyd是一个文科出生,后来自学计算机科学,逆袭成为斯坦福终身教授的大佬。我想这多多少少能证明热爱的力量,也能给可能是非科班出身的你我一些信心吧。
好啦回归正题,“二叉堆”,也就是binary heap,顾名思义,这个数据结构也是建立在一种特别的二叉树上的。
它主要有两个约束:
- 二叉堆是一颗满二叉树。也就是说,除了最后一层外的每一层都没有空节点,且最后一层所有节点靠左排列,不存在从左到右中间有某些节点为空。
- 二叉堆中的 每个节点和其子节点都有一样的偏序关系,要么大于要么小于,这两种情况分别对应大顶堆和小顶堆。所以大顶堆就要求堆中所有节点的值,一定大于其左右子树中的任何一个节点的值,也就是说顶部的节点一定是最大的,故称为大顶堆。小顶堆就正好相反。
有了这样的约束,可以保证根节点要么是最大的要么是最小的,也让我们在出队入队的操作里调整的成本很小,整个过程有点像冒泡排序的感觉,我们马上讲解具体的细节。
比如下图中左边就是一个二叉堆,但中间因为不满足满二叉树的约束,就不是一个二叉堆;右边因为不满足完全的有序关系也不是一个二叉堆。
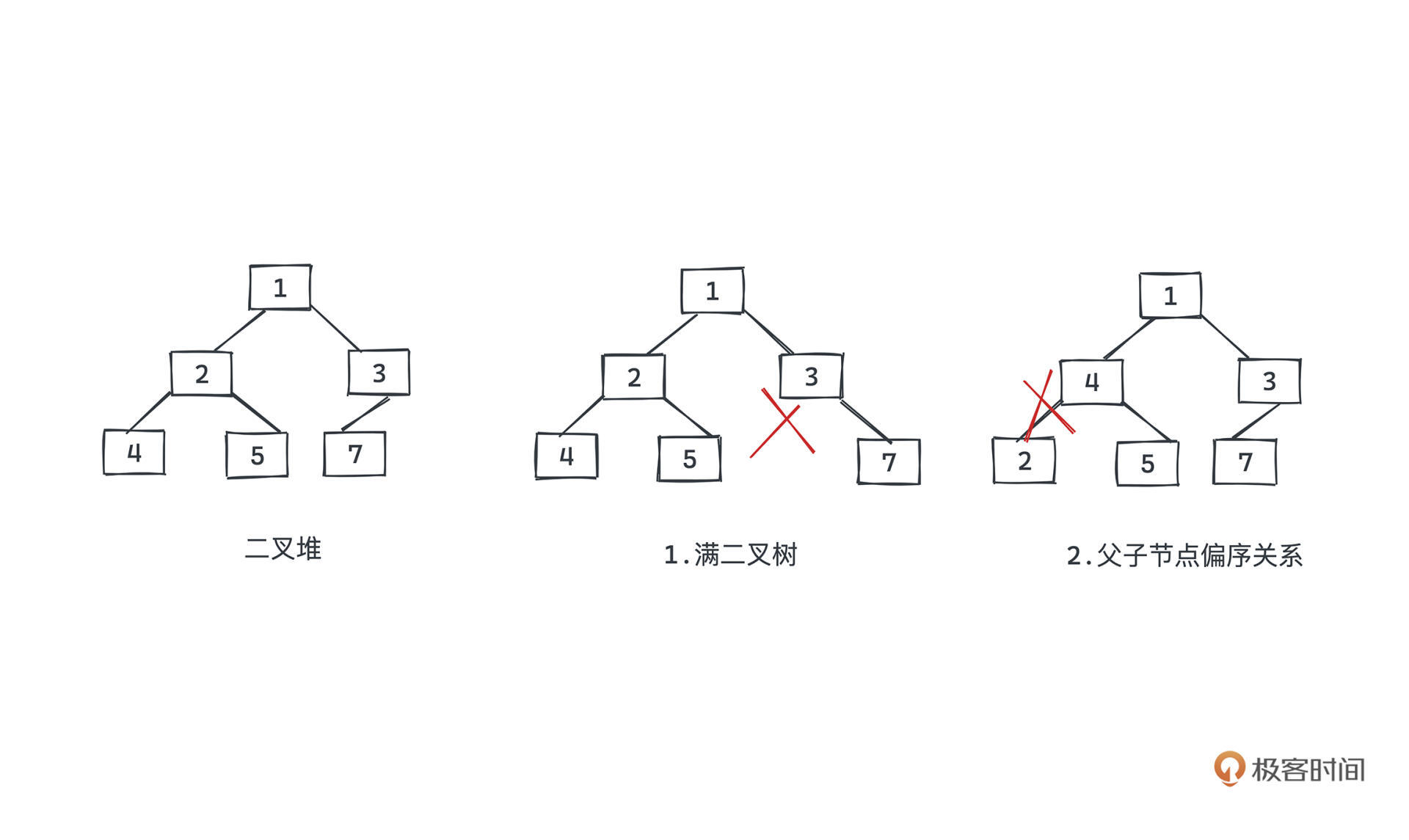
为什么这么设计
那现在我们来看看,这样的数据结构设计对于维护优先队列有什么帮助呢?和红黑树一样,二叉堆这样的树状结构同样暗含了关键的顺序信息,而我们核心就是利用这样的信息,在插入时进行更少的操作,而避免像线性表那样做从头到尾的顺序遍历。
为了实现优先级队列,我们会用优先级,priority,来作为二叉堆节点间大小比较的依据。假设我们始终希望出队的是优先级更高的元素,那可以 采用大顶堆作为优先队列的底层实现,这样每次只需要从顶部取出元素即可获得优先级最高的元素。
当然很重要的一点是,取出元素后显然会在树的顶部产生一个空位,我们需要进行一定的操作使得大顶堆的性质得以保全。
同样,为了享受直接从顶部取出优先级最高元素的便利,我们在插入元素时也要让二叉堆的性质得以保持。
幸运的是,正是因为二叉树是一个满二叉树,其高度约等于LogN,其中N为优先队列中元素的个数。而第二条约束父子节点之间的有序关系,让我们每次做pop和push操作,只需要经过最多二叉树高度次的交换调整即可保持堆的所有特性。
这样,我们就得到了一个入队和出队操作复杂度都为O(LogN)的数据结构,虽然均摊的时间复杂度和红黑树是一样的,但实现的难度却要小很多,所以今天我们就结合源码来讲解。
PriorityQueue的实现
以JDK14中的PriorityQueue为例(后面简称PQ),我们来分析一个生产环境中的优先队列要怎么基于堆实现。
先来看看JDK中优先队列数据结构的基本定义,我们会讲一些重要的成员变量和方法。
public class PriorityQueue<E> extends AbstractQueue<E>
implements java.io.Serializable {
/**
* Priority queue represented as a balanced binary heap: the two
* children of queue[n] are queue[2*n+1] and queue[2*(n+1)]. The
* priority queue is ordered by comparator, or by the elements'
* natural ordering, if comparator is null: For each node n in the
* heap and each descendant d of n, n <= d. The element with the
* lowest value is in queue[0], assuming the queue is nonempty.
*/
transient Object[] queue; // non-private to simplify nested class access
/**
* The number of elements in the priority queue.
*/
int size;
/**
* Inserts the specified element into this priority queue.
*
* @return {@code true} (as specified by {@link Queue#offer})
* @throws ClassCastException if the specified element cannot be
* compared with elements currently in this priority queue
* according to the priority queue's ordering
* @throws NullPointerException if the specified element is null
*/
public boolean offer(E e) { ... }
/**
* Increases the capacity of the array.
*
* @param minCapacity the desired minimum capacity
*/
private void grow(int minCapacity) { ... }
public E peek() {
return (E) queue[0];
}
/**
* Inserts item x at position k, maintaining heap invariant by
* promoting x up the tree until it is greater than or equal to
* its parent, or is the root.
*
* To simplify and speed up coercions and comparisons, the
* Comparable and Comparator versions are separated into different
* methods that are otherwise identical. (Similarly for siftDown.)
*
* @param k the position to fill
* @param x the item to insert
*/
private void siftUp(int k, E x) { ... }
public E poll() { ... }
}
}
首先要看堆元素在内存中到底是怎么存储的。可以看到:
- 成员变量size,它显然用于表示优先队列中元素的大小。
- 成员变量中有一个叫queue的数组,这就是堆中元素存放的地方。
你这个时候可能就会有些疑惑了?诶?那我们堆的树状结构到哪里去了,为什么还是一个线性的存储结构呢?
其实, 在JDK中的PQ实现里,并没有和我们想象中一般的树那样采用节点+指针来实现树状数据结构,而是用了内存上连续的数组来模拟。代码中的queue数组就是用来表示堆这一树状结构的成员变量。
这么讲可能你不是很理解,我们看下面的图。图中画的就是一个大顶堆的示例,上下分别代表堆的树状结构本身和存储到queue数组中的样子。你可以通过元素的值来判断两种表示间的对应关系。
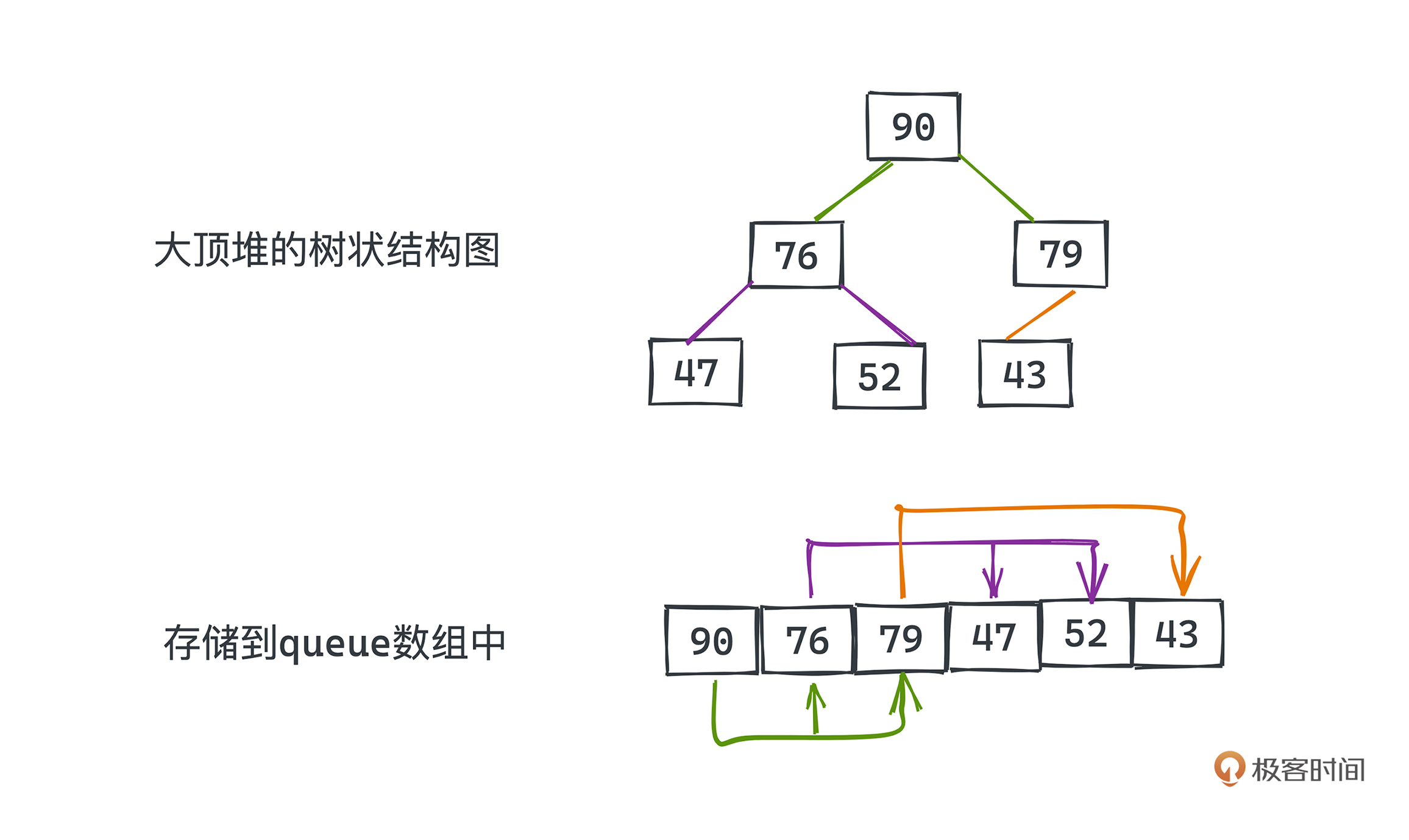
相信你也发现了,图中的数组就是 按照对树做层序遍历的方式依次排列的,所以数组中下标为0的元素就是堆顶的元素,我们也用箭头将数组元素中的父子关系都标记出来了。由于二叉树每一层元素个数都是上一层两倍的特性,你会发现,queue[k]节点,它的左子节点为queue[2 k+1],右子节点为queue[2 k+2]。
事实上,不止二叉堆,其实一般的二叉树也是可以用数组表示的,如果你做过LeetCode上相关试题的话,也会经常碰到类似的表示方式。大部分时候,用数组表示树写起来比较简单,不需要引入类似指针的概念,也不用定义树节点的类或者结构体。
但如果二叉树不是满的,数组中会有大量的空值,非常浪费空间。 而堆本身满二叉树的特性,则让我们可以选择用数组作为底层二叉树实现而不至于浪费大量的内存,这就是JDK中为什么可以使用数组作为底层存储的原因。
堆的操作
有了底层的数据表示,下面我们来了解一下堆的两个重要操作,插入和删除。
首先看堆的插入操作,也就是 offer 方法,对应的代码如下:
/**
* Inserts the specified element into this priority queue.
*
* @return {@code true} (as specified by {@link Queue#offer})
* @throws ClassCastException if the specified element cannot be
* compared with elements currently in this priority queue
* according to the priority queue's ordering
* @throws NullPointerException if the specified element is null
*/
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
grow(i + 1);
siftUp(i, e);
size = i + 1;
return true;
}
该方法接收一个待插入的元素e,在18行中将堆的大小增加1,这个非常直观。有两个函数详细解释一下,grow和siftUp。
grow函数
grow函数用于扩展数组的大小。
我们用数组模拟堆,就必然要给出一个数组的大小,这也就限制了二叉堆的最大大小。但这在使用过程中并不方便,我们没有办法在各种场景下都准确预估堆所需使用的最大元素个数。所以和STL的vector一样,JDK中的PriorityQueue,通过内置的grow函数和扩容机制解决了堆动态大小的问题。grow函数具体做的事情我们最后再讲。
所以在offer方法里,如果发现当前插入的元素已经超过了内置queue数组的容量,我们需要进行扩容操作,这就是第15-16行代码所做的事情。
siftUp函数
现在我们来看siftUp的过程,具体的插入操作其实就隐藏在了siftUp这个函数中。
之所以叫siftUp,就是因为这个插入的过程是自下而上的。我们结合具体例子,来讲解siftUp的过程,先搞清楚思路,再来看对应的代码就很好理解了。
假设有这样的一个二叉堆,我们想要插入一个新的元素。
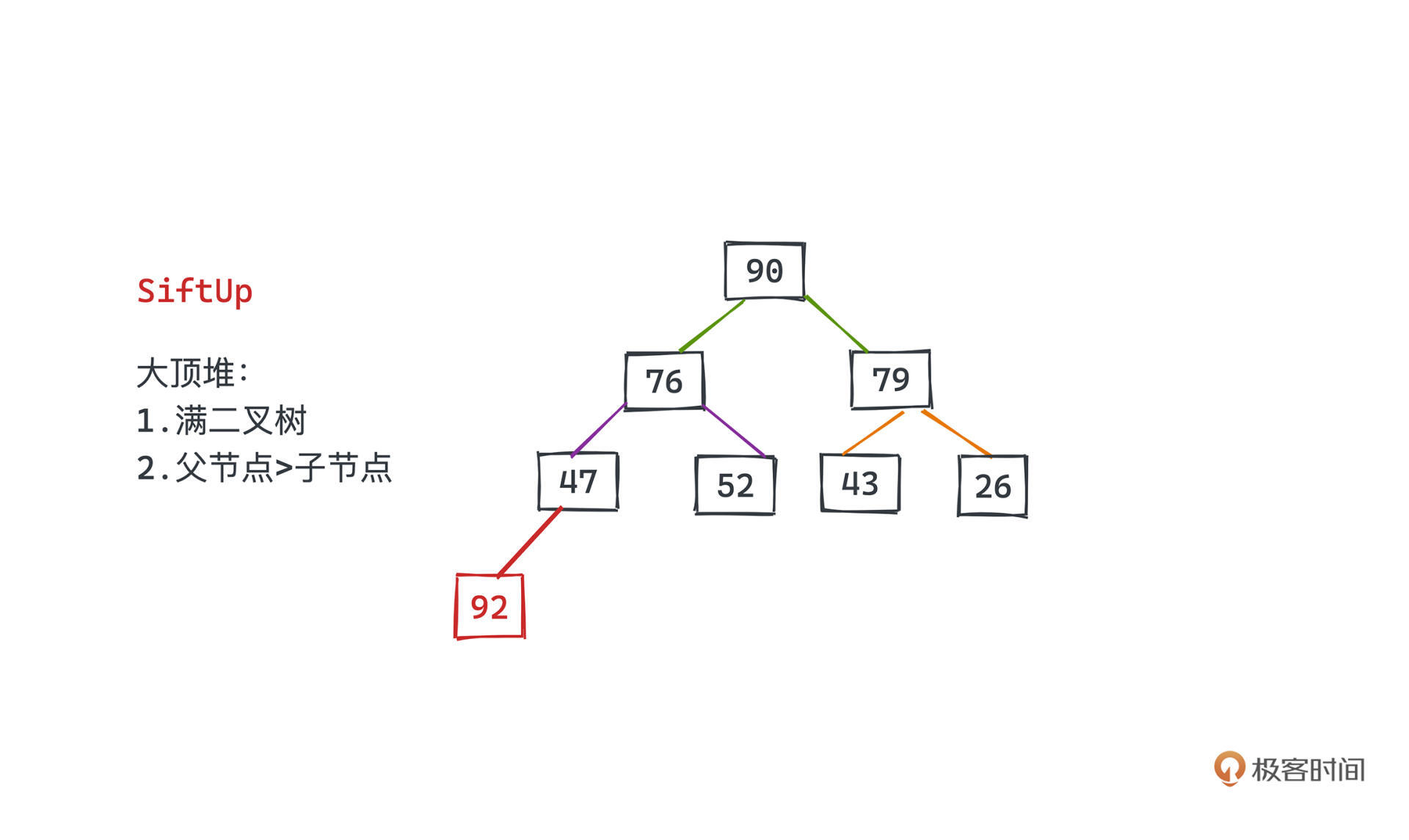
可以先将该元素插入到数组的尾部,也就是堆中的最后一个位置,这是一个O(1)的操作,因为不涉及任何元素的移位。然后要做的,就是将这个元素一路往上交换使得二叉堆可以保持自身的2条特性。
由于我们是将新的元素放到堆的尾部,没有空开任何一个子节点,所以 只是进行元素的交换,并不会破坏堆是满二叉树的特性,因而我们只需要关注父节点比所有子节点大这一特性。
所以将该节点不断和其父节点比较,如果比父节点大,将该节点和父节点交换,并继续和该节点新的父节点进行比较。由于原来的父亲节点一定比其左右子节点(其中一个是这次调整的节点,另一个是他的兄弟节点)都大,所以将其和父亲节点交换位置,一定也能保证该节点比其兄弟节点大。
而只要发现该节点已经比父节点小了,我们就可以结束这次的比较、交换之旅,堆已经重新满足了特性。
结合示意图理解,比如在堆的最后一个位置插入92。
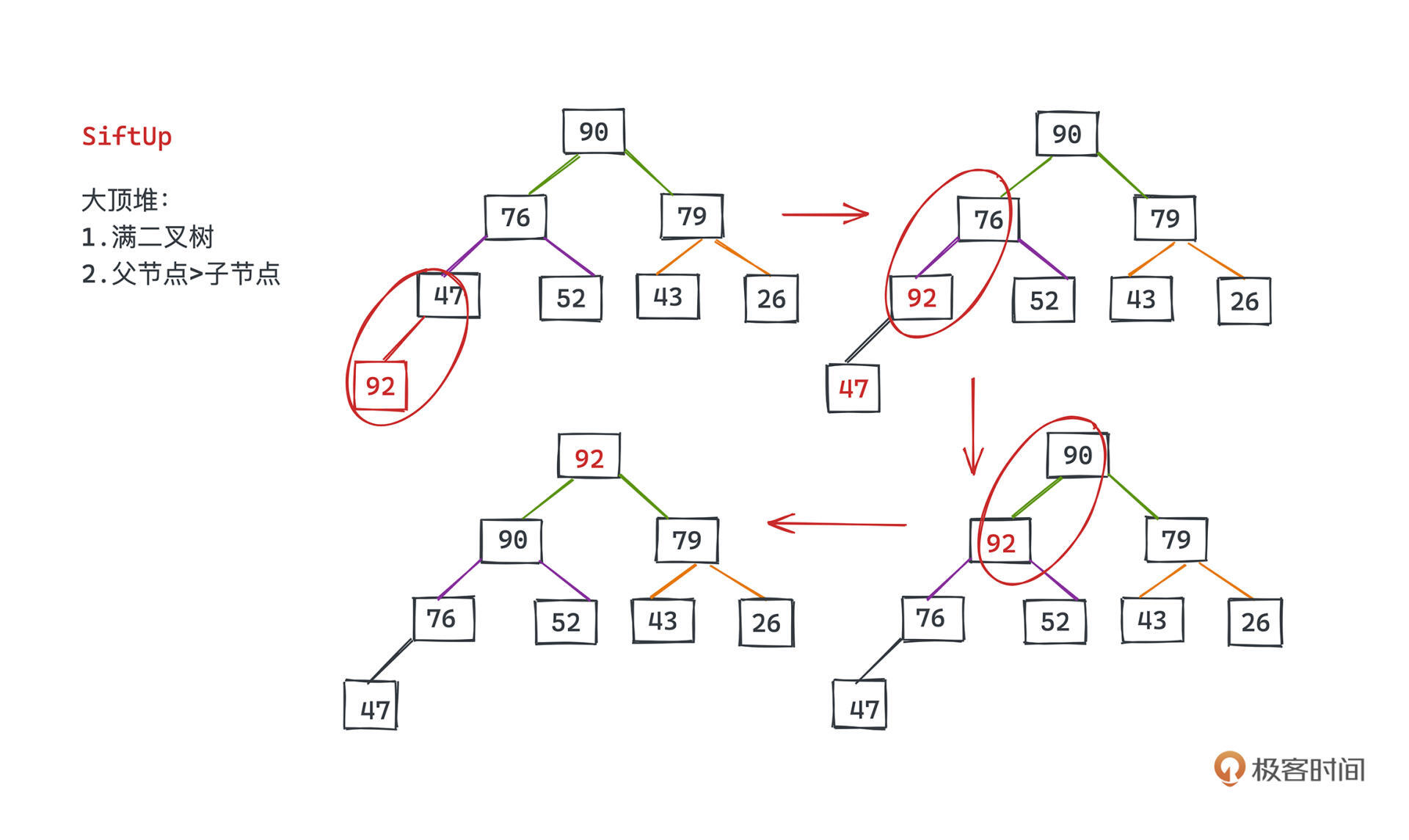
我们要先把92和47比较,发现92比47大的时候,互换位置;然后继续比较,会交换92和76的位置,关注父子节点的大小要求特性,因为76本身比52大,所以交换后一定也能保证92比52。这就是堆siftUp的过程。
这里再稍微补充两句,堆和红黑树不一样,我们在整个过程中只关心父子节点之间的大小关系,而不用在意兄弟节点之间的大小关系,比如原本4(47)节点是比5(52)节点小的,现在4节点(76)比5节点(52)大了,这并不会破坏堆的性质。这也是堆之所以调整比红黑树简单很多的地方。
了解这个过程,对应的代码就非常好懂了。
private void siftUp(int k, E x) {
if (comparator != null)
siftUpUsingComparator(k, x, queue, comparator);
else
siftUpComparable(k, x, queue);
}
private static <T> void siftUpComparable(int k, T x, Object[] es) {
Comparable<? super T> key = (Comparable<? super T>) x;
while (k > 0) {
// 计算父节点的下标
int parent = (k - 1) >>> 1;
Object e = es[parent];
// 比较当前节点和父节点的关系 如果当前节点优先级更高,我们可以直接结束比较
if (key.compareTo((T) e) >= 0)
break;
// 交换节点
es[k] = e;
k = parent;
}
es[k] = key;
}
因为PriorityQueue里存放的可以是任何元素,用户也可以自定义比较关系,所以Java的PQ实现里引入了比较符和泛型的概念。siftUpUsingComparator 则给了用户自定义比较符的自由;不熟悉的同学可以自行搜索相关资料了解。
我们直接看siftUpComparable方法,也就是元素类型自带比较方法的情况。
我们要比较这个新节点和父节点的值,那怎么定位父节点呢?回忆一下前面讲queue底层存储的时候讲过的父子节点关系, 对queue[k]来说,它的父节点一定是queue[(k-1)/2]。当然k需要大于0,否则k就已经是根节点了。
所以11-18行的循环就是在做siftUp中和父节点比较并交换的操作,第14行就是对应key比e大,也就是子节点比父节点大的情况,此时我们就可以退出循环了。这也说明PQ默认情况下实现的是小顶堆。
删除的poll操作
好,下面看PQ中第二个主要操作, poll 操作,这是我们返回并删除堆顶元素的操作,也就是从优先队列中取出最高优先级元素的操作。
public E poll() {
final Object[] es;
final E result;
// 取出堆顶元素
if ((result = (E) ((es = queue)[0])) != null) {
modCount++;
final int n;
// 其实就是要将最后一个元素放到顶部
final E x = (E) es[(n = --size)];
// 将最后一个元素置空
es[n] = null;
// 进行siftdown操作
if (n > 0) {
final Comparator<? super E> cmp;
if ((cmp = comparator) == null)
siftDownComparable(0, x, es, n);
else
siftDownUsingComparator(0, x, es, n, cmp);
}
}
return result;
}
重点理解第7行和关键的siftDown函数。
要取出堆顶元素,数组第一个元素就会有所空缺。基于siftUp的想法(还是用刚才的大顶堆),我们第一反应很容易想到,直接从空缺的根节点开始,找其左右子节点中大的一个提拔到当前空缺的位置,然后依次找新的空位左右子节点哪个位置可以提拔上来,直到没有子节点为止。
这个思路确实很自然,但有一个比较大的问题就是,如果我们在第一次比较的时候选择了左节点提升上来,当右节点并不为空时,最后得到的树一定不是一个满二叉树了,这就破坏了堆的基本性质。
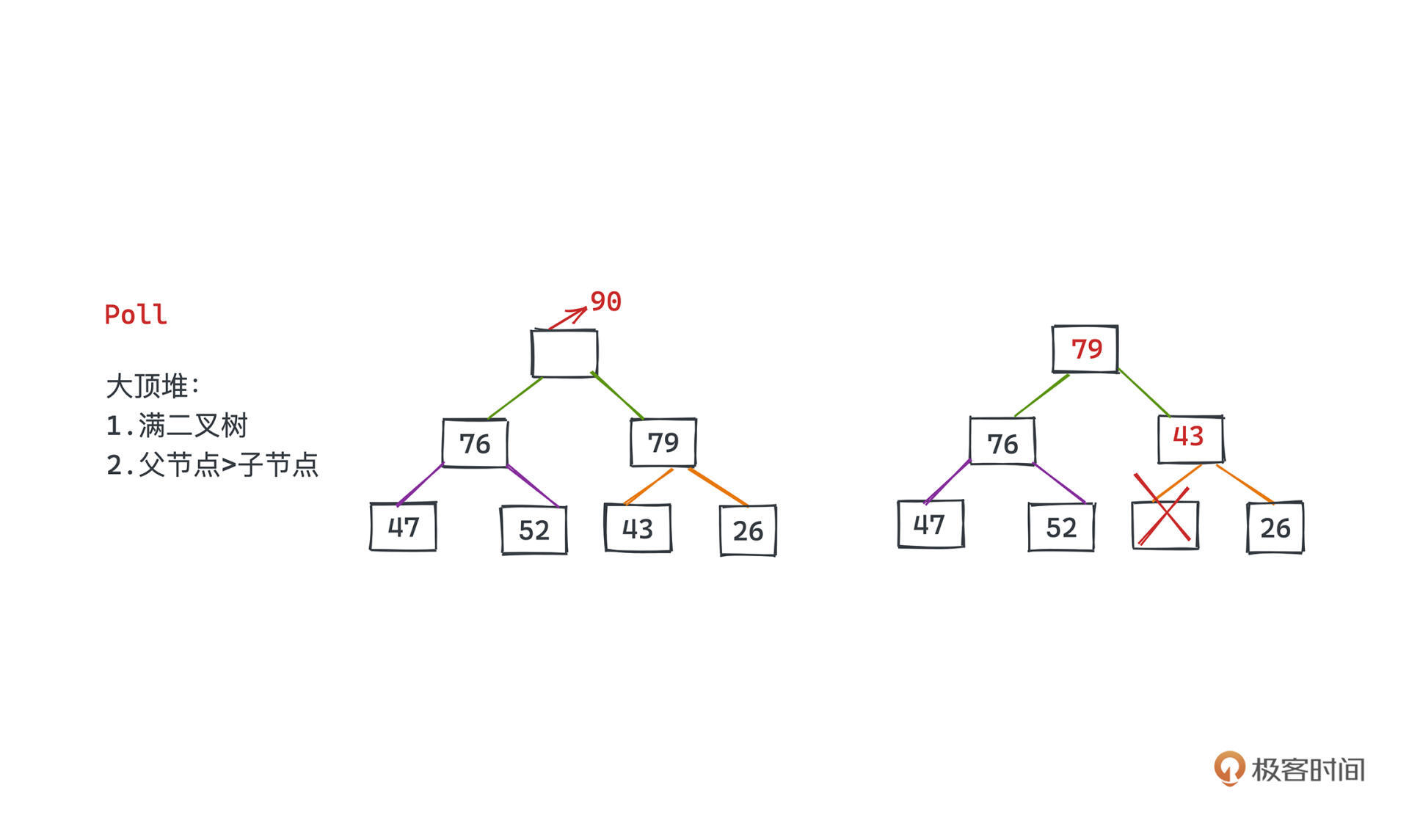
那怎么做呢?一个比较巧妙的想法就是和代码里第7行一样,将根节点删除后,我们把二叉堆中最后的元素提到根节点的位置,这样又可以保证新的二叉树是一颗满二叉树了,然后要做的就和前面所说的一样,比较+交换。
看大顶堆的例子,现在要删掉最大的元素92,怎么做呢?首先把堆中最后一个节点也就是47提到堆顶的空位,然后依次比较左右节点;47比90、79都小,但90更大,所以我们用47和90进行交换。同理47和76也需要交换。这样我们就完成了优先队列优先级最高元素出队的操作。
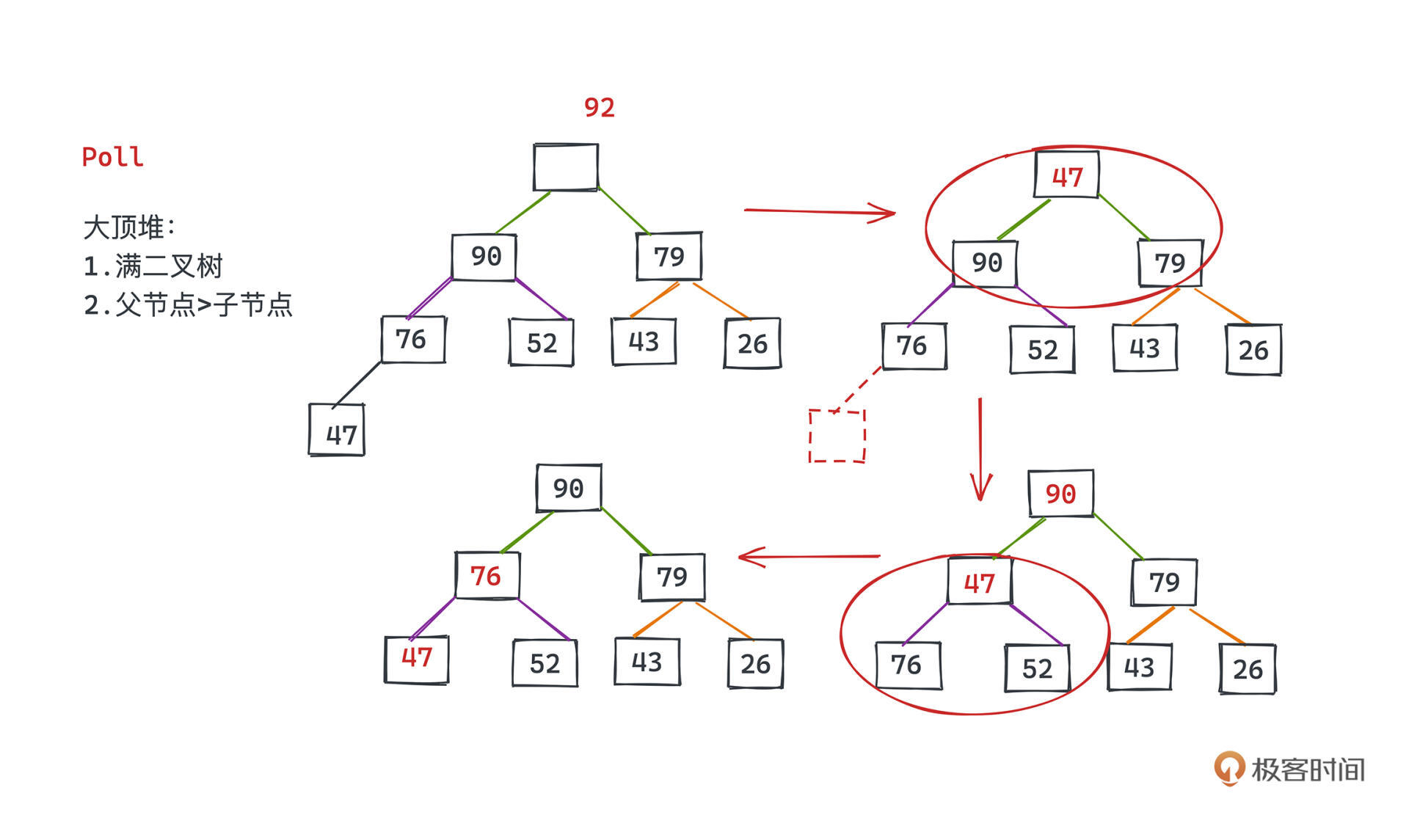
siftDown函数
回到代码,这里说的比较+交换的过程就是由siftDown这个函数完成的:
private static <T> void siftDownComparable(int k, T x, Object[] es, int n) {
// assert n > 0;
Comparable<? super T> key = (Comparable<? super T>)x;
int half = n >>> 1; // loop while a non-leaf
while (k < half) {
int child = (k << 1) + 1; // assume left child is least
Object c = es[child];
int right = child + 1;
if (right < n &&
((Comparable<? super T>) c).compareTo((T) es[right]) > 0)
c = es[child = right];
if (key.compareTo((T) c) <= 0)
break;
es[k] = c;
k = child;
}
es[k] = key;
}
5-14行就是之前所说的父亲节点和左右子节点循环比较并交换的过程。k的左子节点下标为(k<<1)+1,右子节点下标为左子节点+1,这就是6行和8行代码的意义。在发现左右子节点都比根节点小之后,同样可以退出循环,否则和左右节点中小的一个交换即可。
嗯,如果只是要查看优先级最高的节点而不用出队,当然是非常简单了,我们直接取堆顶元素即可。也就是之前PQ定义的这几行代码:
public E peek() {
return (E) queue[0];
}
扩容机制
那,最后我们来讲讲PQ的扩容机制,这是PQ虽然用数组作为底层存储,却不用限制优先队列大小的核心。
/**
* Increases the capacity of the array.
*
* @param minCapacity the desired minimum capacity
*/
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// Double size if small; else grow by 50%
int newCapacity = ArraysSupport.newLength(oldCapacity,
minCapacity - oldCapacity, /* minimum growth */
oldCapacity < 64 ? oldCapacity + 2 : oldCapacity >> 1
/* preferred growth */);
queue = Arrays.copyOf(queue, newCapacity);
}
本质和之前讲的STL中的vector扩容思想如出一辙,就是将当前的数组搬到一段更大的连续数组中,新的数组容量为newCapacity,旧的数组容量为oldCapacity。
它俩的关系在第11行中可以看出来:如果原来的数组已经比较大了,那新数组的大小是旧数组大小的1.5倍,否则是2倍再+2。至于为什么要成倍增长,你可以回看vector的章节,都是为了保证良好的均摊时间复杂度。
用于计算容量的newLength的方法还有个参数用于保证最小的扩容大小,如果你感兴趣可以自己研究一下。
总结
学完了JDK中PriorityQueue的主要实现机制和源码,现在你有没有掌握用数组模拟树的技巧呢?如果让你手写一个堆应该也不难了吧,这也是面试中算法的常考题目。
核心就是数组中父子节点的下标关系。下标为k的节点queue[k],它的左子节点为queue[2 k+1],右子节点为queue[2 k+2]。理解了这一点,去实现siftDown和siftUp操作,相信对你来说不在话下。
当然JDK为了提供一个更通用的优先队列,也引入了泛型,也提供了动态扩容的能力,这些内容和动态数组的实现非常相似的,你可以回去复习并尝试手写实现一下。
课后作业
有了堆,实现优先队列的语义其实并不难。但有个问题想问问你,你觉得Java的优先队列是否真正保证了优先队列语义呢?比如优先队列中相同优先级的元素,是否应该要保证先进先出的特性?如果,JDK中的没有这个保证,但我们却有这样的需求,你觉得应该如何改造呢?
这是一个开放问题,欢迎你在留言区参与讨论。如果你觉得这篇文章对你有帮助,也欢迎你转发给身边的朋友一起学习。我们下节课见~