business-algorithm-course

02｜双向链表：list如何实现高效地插入与删除？

你好，我是微扰君。

在上一讲实现的一个简易银行账户管理系统中，每个账号都对应了一个余额，系统支持用户的开通、存/取款和查询余额。我们使用动态数组容器满足了频繁随机访问查询的需求。

但是如果要在系统里支持删除的功能，就会有一个问题：我们为了不进行整体的数组移动操作，通常就只能保留这个用户在数组里占用的内存，用将元素标记为特殊值的方式来模拟“删除”；而因为数组是连续存储的，不能单独释放掉数组中间某些区域的内存，所以这段内存空间我们实际上就是浪费的。

如果还有个需求，比如现在某个不讲道理的领导来到这个银行，要求自己在数组中排在最前面；那么我们不得不将所有人的账户信息往后挪动一位来满足他奇怪的自尊心，这也会带来高昂的时间复杂度。

那么有没有办法让我们不再需要连续的存储空间去存储一个序列，同时又可以在序列中快速进行插入/删除操作而不用波及之后的所有元素呢？

这就需要另一种常见的序列式数据结构——链表登场了，这同样是几乎所有高级语言都会原生支持的数据结构。

链表

链表这个数据结构的发明也是很久之前的事了，最早在1955年，它就是IPL这一古老语言的内置数据结构，用于开发当时的人工智能程序。

类似数组，链表同样是一种序列式的数据结构，但存储元素时并不需要使用连续的内存空间，而是采用一系列通过指针相连的节点来存储， 因为有了指针来关联节点的地址，就不需要连续存储了。

在每个节点内，我们都会同时存储元素的数据信息和一个指针，存储元素信息的部分是数据域，也就是 data field，存储指针的地方称为引用域，也就是 reference field；其中指针指向该节点的后继节点，也就是记录着链表中存储下一个元素节点的地址。

下图就是一个典型长度为3的链表的示例，我们可以通过指针很容易地从第一个节点遍历完整个链表。

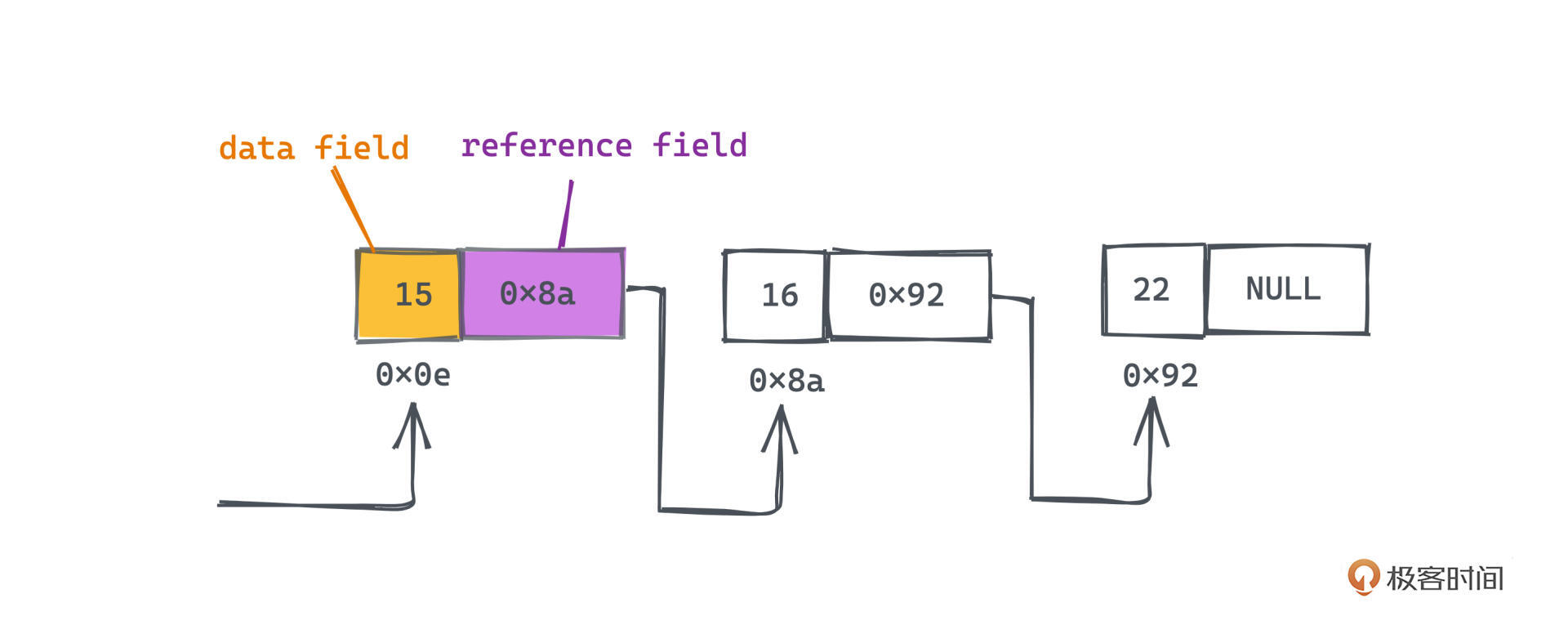
从内存布局能看出来，链表比连续存储的数组，有更灵活的内存使用方式和更高的内存使用率。

因为数组要求事先分配内存，而链表是每次插入新节点的时候，才申请该节点所需的内存空间，灵活得多，也就不会有分配空间没有被使用的浪费问题，自然内存使用率高。

链表存储元素采用的是通过指针的串联方式，而非数组的连续排列方式。我们在任何位置插入或者删除节点，不再需要为了保持元素的连续存储而进行O(n)的整体移动操作，只需要进行O(1)的指针改写，加申请或者释放内存就行。这显然比数组的插入删除要高效得多。

但是毕竟鱼和熊掌不能兼得。 也正是因为这样非连续的存储方式，我们需要访问链表中第n个元素的时候就不得不从头节点遍历，导致访问第i个元素的均摊时间复杂度为O(N)，而不能像数组那样直接基于下标和元素大小，计算出指定元素的偏移量。

所以，我们并不能简单地说链表和数组哪个更好，而是要根据使用的场景做出合适的选择。毕竟如果两个相似的数据结构其中一个各个方面都好于另一个的话，另一个数据结构可能也不会存在至今了。

基于上面的特性对比，我们可以得出一个大致的结论：链表更适用于删除、插入、遍历操作频繁的场景，而不适用于随机访问索引频繁的场景。比如在内存池、操作系统进程管理、最常用的缓存替换算法LRU中都有应用，之后讲解到相关专题的时候也会提到。

单链表vs双链表vs循环链表

在实际使用过程中，根据不同的需求，大致有3种常见的链表形式，单链表、双链表和循环链表，它们都需要支持几种最基本的链表操作，包括插入节点、删除节点、修改节点信息，以及访问遍历节点信息。

可以看图直观感受三者的区别。三种链表节点都包含引用域和数据域。

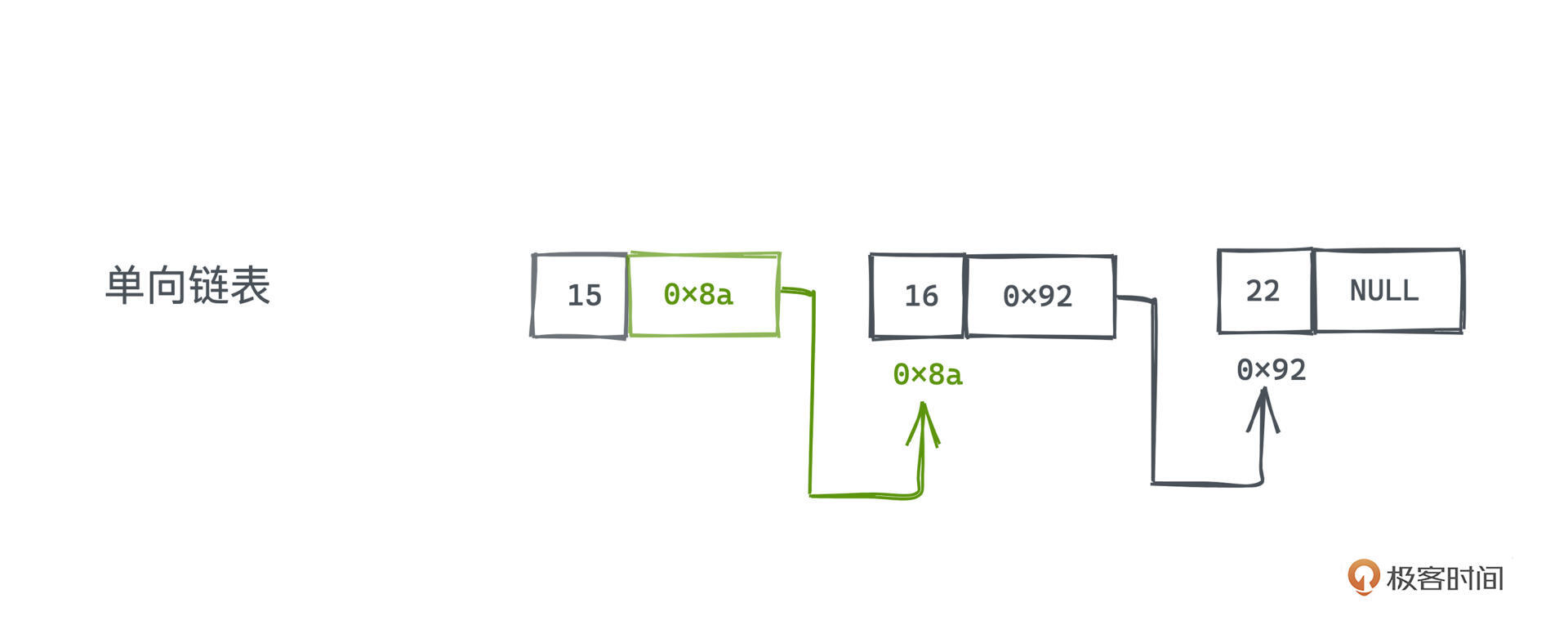
其中，单链表和双链表最大的区别就在于，单链表的引用域，只存了一个后继指针。

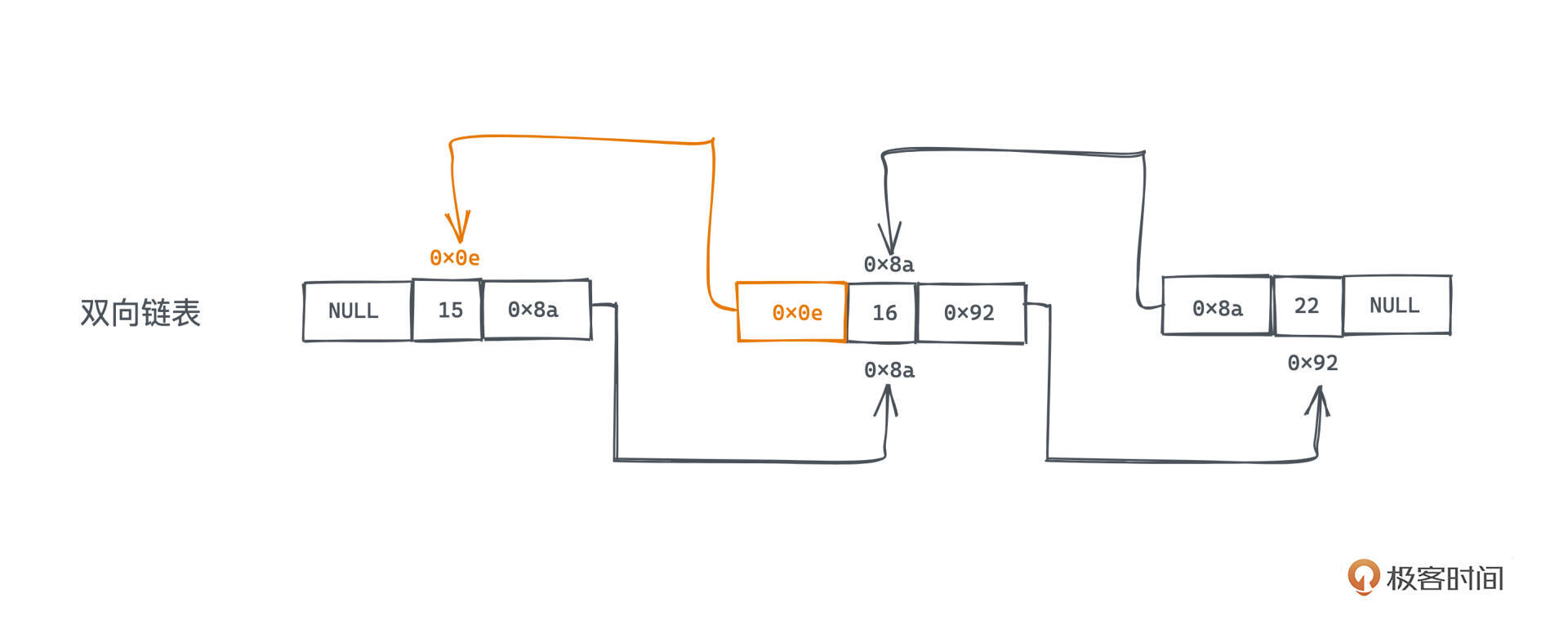
而双链表有两个引用域，不只存有后继节点的地址，也存储了前驱节点的信息，这使得我们 可以双向遍历链表，拥有了在遍历中回退的能力。在链表首尾的前驱和后继指针，可以设为NULL或者指向一个特殊的虚拟节点，来标记链表的终结。

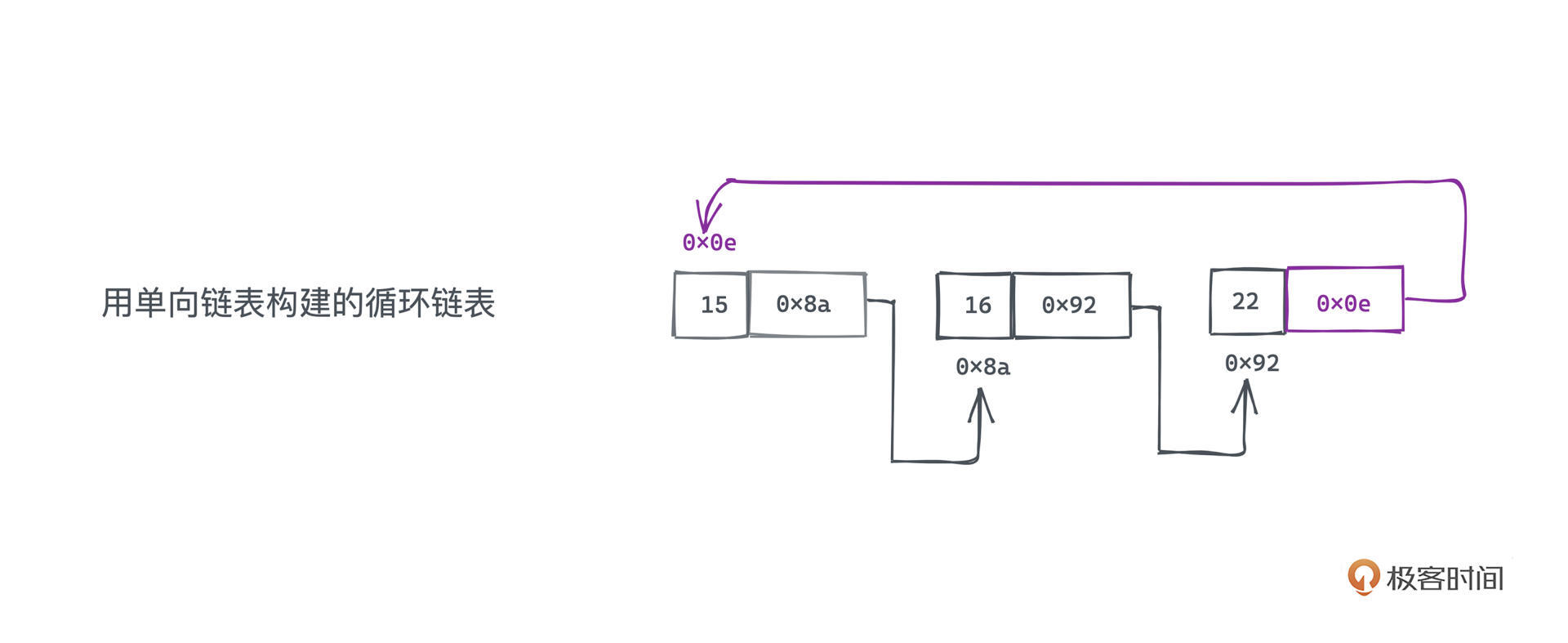
而循环链表则是一个没有边界的环，既可以用双链表来实现也可以用单链表实现。相比于前两者的主要区别在于，在链表的边界，比如尾部，不再设为NULL或者一个虚拟节点，而是直接将尾部指向链表的头部。这在许多需要循环遍历的场景下非常有用，比如可以用于模拟约瑟夫环。

STL中List的实现

好了，讲解完链表的基础概念和分类，进入今天的重头戏，我们看看如何实现一个链表。

为了契合专栏真实世界的语义，我们继续以STL这一久经考验的C++标准库中的实现来讲解。 List就是STL中的链表容器，它实现的是前面提到的双向、循环链表。如果你想要使用更节约空间的单链表，STL中也提供了相应的实现 forward_list，有兴趣的话，你可以自己去了解背后的实现。

和上节课一样，因为STL的实现背后涉及了许多繁琐的C++高级语法，我们会对代码做一定的简化方便理解，你对C++不感兴趣的话也不用深究。

链表节点的实现

首先来看一下 list 的主要组成部分node ，也就是链表节点，它是整个链表的关键，存储着元素信息本身和连接链表的前后指针。

Node节点的实现如下：

template <class T>
struct __list_node {
  __list_node<T>* next;  // 前驱节点指针
  __list_node<T>* prev; // 后继节点指针
  T data; //存储数据
};

可以看到，链表节点的定义，除了为了支持各种元素类型而用到的泛型语法。其他的内容和前面说的双链表的节点完全一致， 指针域同时包含了前驱和后继节点的地址，成员变量data用于存储元素信息本身。

链表迭代器的实现

所有的STL容器都需要实现迭代器，这也是后面所有操作的基础。

迭代器提供用于遍历的最重要的接口，它本身也是一种重要的设计模式，支持的操作就是自增 ++ 和自减 --。上一讲的vector，因为内存是连续存储的，可以直接通过地址的++和–操作；但在内存不连续存储的List中，我们需要基于节点引用域中的前驱后继节点信息，来实现自己的迭代方法。

代码如下：

template<typename T>
struct __list_iterator{
    typedef __list_iterator<T>   self;
    typedef __list_node<T>*      link_type;
    link_type ptr; //成员
    __list_iterator(link_type p = nullptr):ptr(p){}
}

T& operator *(){return ptr->data;}
T* operator ->(){return &(operator*());}
// 类似 ++x 返回next节点
self& operator++(){
    ptr = ptr->next;
    return *this;
}
// 类似 x++ 返回当前节点
self operator++(int){
    self tmp = *this;
    ++*this;
    return tmp;
}
// 类似 --x 返回prev节点
self& operator--(){
    ptr = ptr->prev;
    return *this;
}
// 类似 x-- 返回当前节点
self operator--(int){
    self tmp = *this;
    --*this;
    return tmp;
}
bool operator==(const __list_iterator& rhs){
    return ptr == rhs.ptr;
}
bool operator!=(const __list_iterator& rhs){
    return !(*this==rhs);
}

其实就是将迭代器的方法都实现一遍。我们重点需要关注的操作是++和–，对应实现也非常直观。

在迭代器中，ptr是我们的主要成员变量，它指向的就是迭代器当前遍历的节点地址。所以++就是返回一个指向 ptr->next 的指针；而–对应的，就是返回一个指向 prt->prev 的指针；同时我们需要把内置的ptr 也指向prt->next 或者 ptr->prev。这样我们就可以自如地用迭代器在链表上进行遍历了。

链表数据结构的实现

有了迭代器和节点，我们要做的就是将STL中双向循环链表的结构，用C++语言描述出来，并将一些链表相关的基本操作实现出来。

所谓链表，就是要将节点链接起来。由于链表节点本身已经存了前置后继节点的地址，所以 链表数据结构主要的内涵，其实只需要使用一个节点即可表示出来，用这一个节点，我们就可以找到所有其他的节点。

所以数据结构定义如下：

    template<typename T>
    class list{
        protected:
            typedef __list_node<T> list_node; // 显示定义list_node类型
            typedef allocator<list_node> nodeAllocator; // 定义allocator类型
        public:
            typedef T                  value_type;
            typedef T&                 reference;
            typedef value_type*        pointer;
            typedef list_node*         link_type;
            typedef const value_type*  const_pointer;
            typedef size_t             size_type;
        public:
            typedef __list_iterator<value_type> iterator; // 迭代器类型重写
        private:
            link_type node; // 只要一个指针，便可表示整个环状双向链表
            // ......
    }

这段代码看起来比较长，其实大部分是一些类型定义，比如简写了带泛型的节点类型，更多是为了保证语义清晰和可读。我们真正要关注的只有private的成员变量 node，事实上，这一个节点就可以表示整个环状双向链表。

在内存中的排布方式如下图所示：

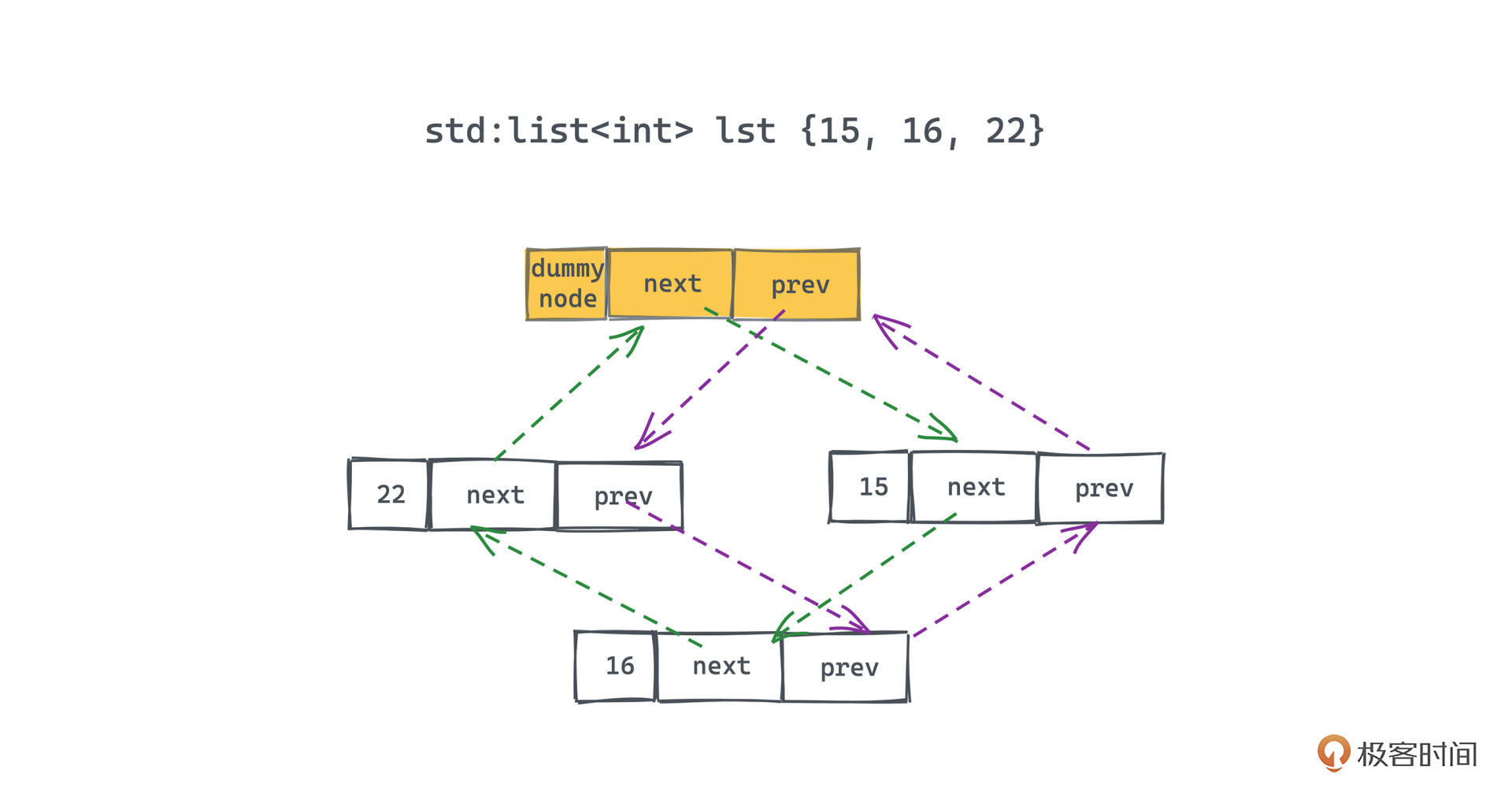
每个链表数据结构，都会有一个 虚拟节点的成员变量node，用于标记这整个循环链表的首尾连接处，它既是整个链表的开始，也是整个链表的结尾；也就是说，这个虚拟节点的pre 指向链表的最后一个节点，它的next指向链表的第一个节点。

所以链表初始化容量为零的时候，显然只有一个前后指针都指向自己的虚拟节点。

这里还有一个非常巧妙的设计，我们会让end()迭代器指向这个虚拟节点，begin()则会指向虚拟节点的下一个节点，这完美符合迭代器前闭后开的语义。

因为end()节点指向的是一个并不真实存储数据的元素，是永远取不到值的；而对应的begin()，在链表不空的时候，指向正是链表中的第一个节点。因此要遍历链表所有的元素的时候，就会写出这样的代码：

for (std::list<int>::iterator it=mylist.begin(); it != mylist.end(); ++it)
    std::cout << ' ' << *it;

我们在判断是否遍历到终点的代码，就和vector一样，写的是 it != mylist.end() 。

链表基本操作的实现

好了，终于来到最激动人心的部分：链表的基本操作。

有了刚才的数据结构和迭代器，很容易访问到链表的节点了，我们开始实现链表的另外几个主要操作：初始化链表、插入节点、删除节点。

先来看一切的开始，链表是如何初始化的。

相比数组其实要简单一些，因为前面说了，一个空的链表，就只包含了一个虚拟节点，STL内置的空间配置器很容易处理这个节点的内存申请。初始化代码如下：

void empty_initialize() {
  node = get_node(0);
  node->next = node; // next 指针指向自身
  node->prev = node; // prev 指针指向自身
}

link_type get_node() { return list_node_allocator:allocate(); }

当链表为空时，虚拟节点前、后指针都指向自身，代码就是如此简洁直观。

那怎么往链表里插入数据呢，我们主要看 insert 方法是如何实现的，它用来在链表中的任何一个节点后面插入数据。有了insert，我们当然也能很容易实现 push_back 等常用方法。

那 insert 需要传入哪些参数呢？

前面也说了，相比数组，链表的最大优势之一就是它的插入和删除效率会高效得多。这正是因为内存空间不是线性排列的，所以想要插入数据，我们只需要修改指定位置的前、后指针的指向，把新的节点在逻辑上插入某个位置就可以了。

所以 insert需要 两个入参，一个是插入位置，类型是一个迭代器；另一个是插入的值。其实现方法如下：

iterator insert(iterator position, const T& x) {
  lik_type tmp = create_node(x); // 创建一个临时节点
  tmp->next = position.node; // 将该节点的后继指针指向当前位置的节点
  tmp->prev = position.node->prev; // 将该节点的前驱指针指向当前位置的前驱节点
  (link_type(position.node->prev))->next = tmp; // 将前驱节点本来指向当前节点的后继指针改为指向该临时节点
  position.node->prev = tmp; // 同样，当前位置的前驱指针也要修改为指向该临时节点
  return tmp;
}

代码其实并不复杂，但许多新手还是需要花一些时间理解一下的，整个过程有点像“穿针引线”。

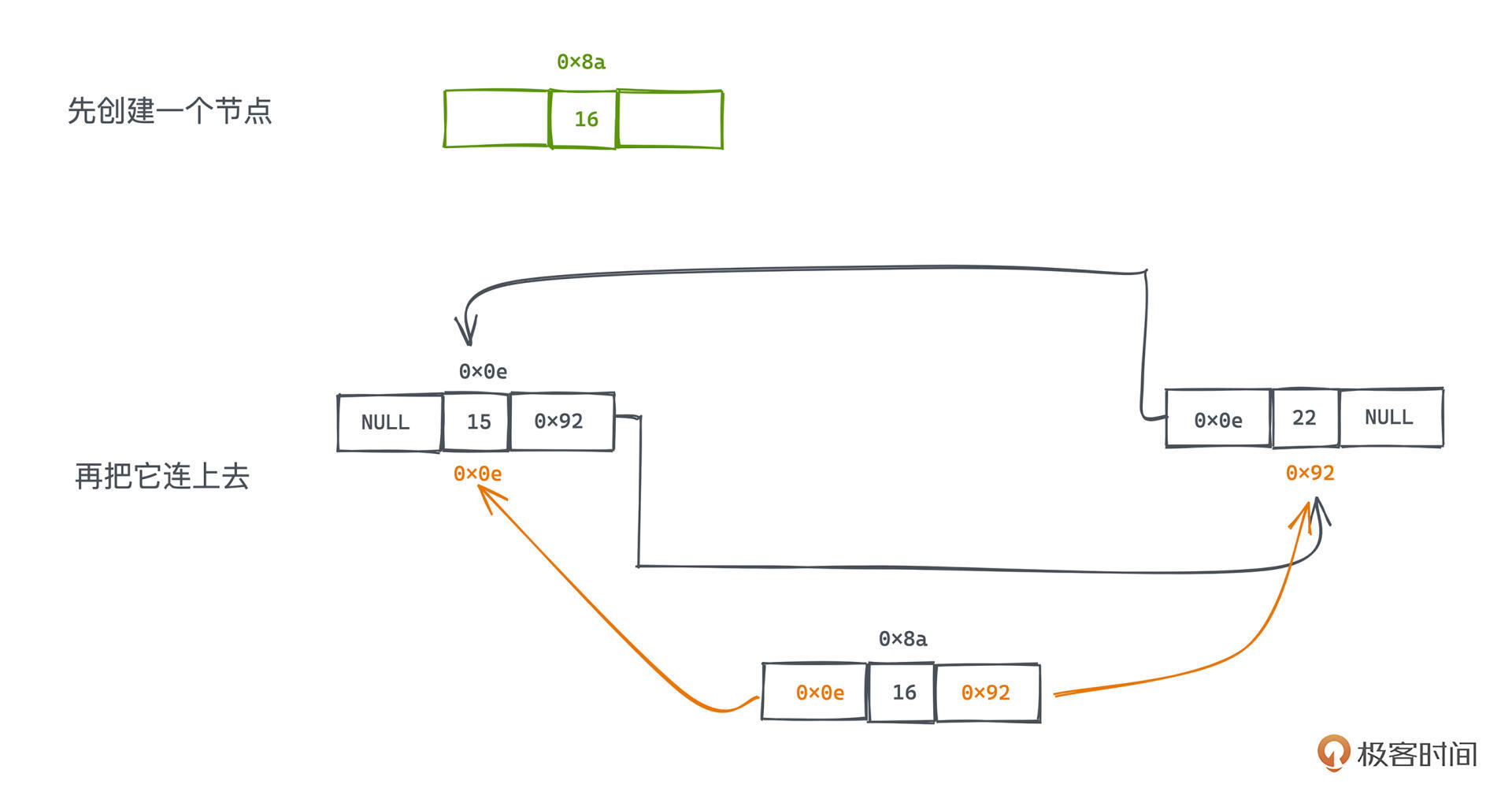
先创建一个节点tmp，将该节点的前驱后继分别指向当前position的前驱和position本身；再将当前position的后继和position->prev的前驱指向这个新创建的节点。这样我们就完成了链表节点的插入。

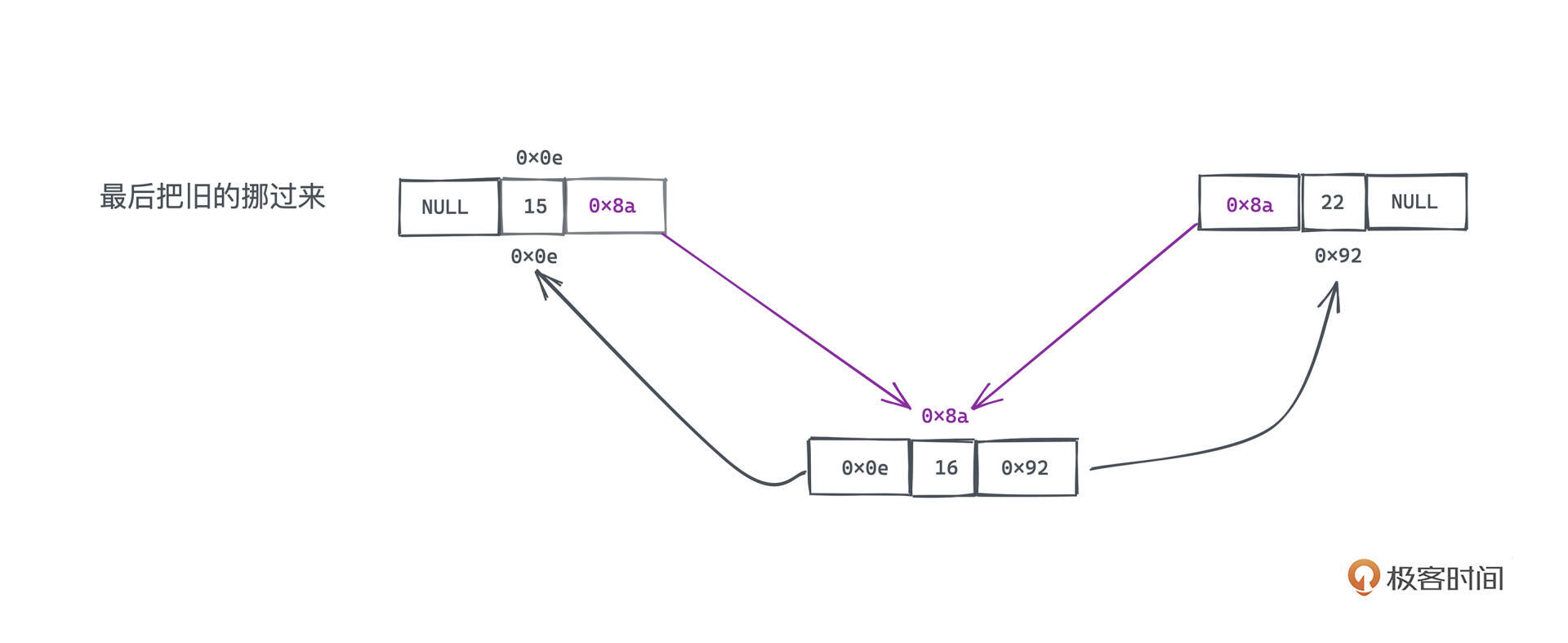
这些操作的顺序是非常重要的。你可以理解成要 先把新的节点全接上去，才能把旧指针一一改过来。

如果调换了操作的顺序，比如先将当前position的后继指向临时节点，那么我们就访问不到插入节点的后继节点了。建议你用纸笔多模拟几遍整个插入的过程，多练习几遍自然就能掌握了。

而链表的删除操作是类似的，基本上就是进行一组和插入相反的操作。找到某个需要删除的节点位置，将该节点的后继和前驱直接关联在一起，最后释放掉待删除节点的空间即可。代码如下：

iterator erase(iterator position) {
  link_type next_node = link_type(position.node->next);
  link_type prev_node = link_type(position.node->prev);
  prev_node->next = next_node;
  next_node->prev = prev_node;
  destroy_node(position.node);
  return iterator(next_node);
}

有了 insert 和 erase操作，其他一些基础操作当然也很容易衍生出来。比如pop_front/pop_back/push_back，我们只需要在指定的位置调用 erase 和 insert 即可，首尾的位置都可以通过begin、end等迭代器接口快速取到：

void pop_front() { erase(begin()) };
void pop_back() {
  iterator tmp = end();
  erase(--tmp);
}

push_back(const T& x) { insert(end(), x); }

这三个操作都是在O(1)时间复杂度内可以完成的，比vector对应的操作O(n)的时间复杂度要高效很多。

list其实还支持sort等操作，借助内部实现的transfer方法和归并排序的思想，同样可以做到O(n*logn)的复杂度。但实现比较复杂，如果你有兴趣，可以去看自己搜索一下相关的资料，力扣上有一道关于链表排序的 题目 也可以练习。

总结

链表，相比于数组，有更好的灵活性和更低的插入、删除的复杂度，更加适用于查询索引较少、遍历、插入、删除操作较多的场景，所以要频繁在容器中间某个位置插入元素的时候，就经常用到，比如在LRU和操作系统进程调度的场景下就都会用到。

链表操作在实现的过程中主要需要注意指针之间的变换顺序，你可以在脑海里多模拟几遍这样的过程，并尝试在不借助参考资料的前提下自己实现几次，这也是面试官在算法面试中经常会考察的点。

课后作业

今天没有讲链表中find方法的实现，这也是STL在各种容器中都会提供的一个通用方法。该方法用于寻找容器中某个值的迭代器，比如链表 1->5->3->4 中，调用find(3)，你应该返回的就是链表中的第三个节点的迭代器。你可以来实现一下find方法吗？时间复杂度又是多少呢？

欢迎留言与我讨论。如果你觉得文章有帮助的话呢，也欢迎你点赞转发，我们下节课见～